From this point on things tend to get a bit out of hand. The remaining symmetry subgroups are small and don't place many restrictions, so there will be many patterns in each section.

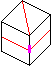
18. Symmetry m_fr2_e, <(24), (13)(24)>, 4.

Suppose the r2 symmetry is centred around the FR/BL middle layer edges, and that a plane of reflectional m symmetry goes through the middle layer.

The corners lie in three orbits: {UFR,DFR} {UBL,DBL} and {UFL,UBR,DFL,DBR}. Not only can they move just as in section 9 (9a-c), a single corner swap (UFR,DFR) is possible if there is an odd edge permutation to combine it with.

Only one corner orbit can be twisted:

1. 4-twist of corners, type 1 UBR+,DBR-,UFL-,DFL+
   L' B' R B R2 U2 B' U2 Fa R' F' L R2 U2 (15f*)
   D' F Ra B2 Ua' F' Ra B Ua' Ra B' U' (18q*)

The U/D edges lie in two orbits, of 4 edges. These can be moved in three ways:

2. 2-swap of edges, type 4 (UR,DR)(UF,DF)
   (F2 R2)³ (6f*,12q*)
3. 2-swap of edges, type 5 (UR,DF)(UF,DR)
   U R2 F2 R2 U2 F2 R2 F2 U (9f*)
4. 2-swap of edges, type 6, [p166] (18b+18c) (UF,UR)(DF,DR)
   R2 U R2 F2 R2 U2 F2 R2 F2 U R2 (11f*)
   U' Rs' F2 Us' R Us Rs U2 (11q*)

The two orbits can be swapped, by 5h for example. They can be flipped too:

5. 4-flip of edges, type 2 {UF+,UR+,DF+,DR+}
   R F2 R2 F R2 F2 R' U2 B2 L2 D L2 B2 U2 (14f*)
   U' Rs F Us' Fs' U' Fs' R' Us Rs U2 (18q*)

The middle layer edges lie in two orbits, in opposite pairs. Each orbit can be flipped by 9f, and a single pair can be swapped if it is combined with the single corner swap mentioned above:

6. Corner swap and edge swap (FL,RB)(UFR,DRF)
   R U2 F U2 R' U R2 U F' U' R2 F2 R F2 U' (15f*)
   F R F R' F2 U R' B U B' U' F U F' R U' (17q*)

These patterns form a group of order 98,304 (= 2¹⁵3).

An easy way to generate the nice patterns is to do a nice pattern from section 9, and then perform one or more of 18b/c/d/f so as to spoil its extra r2 symmetry. Lets first list all nice patterns involving 18f.

7. (18f+9b')
   F R2 F2 L B2 R U R' U' B2 R' D L' F2 R' F' (16f*)
   U F2 U' F' U' R U B D' R' F R D B' F' R F R' (19q*)
8. (18f+9f')
   F U L D2 B U2 R B' D B2 U2 L2 B2 D F L' U' (17f*)
9. (18f+9b'+9f')
   R' B2 L' U' L2 F L2 F2 L2 Us' R' U' B D2 F' R2 U' (18f*)
10. (18f+18b)
    U B2 L B L D' L2 D B D' R F' D F' R' Us' (17f*)
11. (18f+9b'+18b)
    L B' D2 F2 D F2 R2 B F2 D B' F2 R2 B D' L' (16f*)
12. (18f+9f'+18b)
    B2 R' D B U' L2 F' R D' R' F' R2 B F2 Us R' (17f*)
13. (18f+9b'+9f'+18b)
    R F' Ua' L' D' L U2 L U L' U B' D2 U F' R' (17f*,19q*)
14. (18f+18b')
    U' B2 D2 L2 U F2 L2 U L D' F D2 F' D L' B2 R2 U2 (18f*)
15. (18f+9b'+18b')
    L2 R F2 R2 B' L2 F D F' D' L2 F' U B' R2 F' R' (17f*)
16. (18f+9f'+18b')
    B R Us' B R2 F2 L' R2 U' L2 U' B' D' B U' R' (17f*)
17. (18f+9b'+9f'+18b')
    R' B2 U2 R2 F D' R2 U' B2 D' F L' D L F' R F' U' (18f*)
18. (18f+18b+18b')
    B L D' U L U R2 D2 L D2 U' R2 B U R F2 R' U' (18f*)
19. (18f+9b'+18b+18b')
    R F' U2 B' R2 U2 B' D2 U' F' U2 B2 U R2 B U2 R' (17f*)
20. (18f+9f'+18b+18b')
    D2 F2 U' B2 L2 D' Fa' L U2 B2 R Ua' B' Ra' U2 (18f*)
21. (18f+9b'+9f'+18b+18b')
    F2 L R2 U F2 L D' B R2 B2 D' L' F2 U2 B2 U' R' U2 (18f*)
22. (18f+18d)
    R2 D2 B2 Us B2 D' R F' U F2 U' F R U2 (15f*)
23. (18f+9b'+18d)
    U2 R2 U2 F2 U2 F2 U R' F D' F2 D F' R' U2 (15f*)
24. (18f+9f'+18d)
    B' L U' Fs2 D L D2 L R2 U' B' R2 B' L2 B' L' (17f*)
25. (18f+9b'+9f'+18d)
    L F D B' L2 U2 R2 F D' B' R' D2 R2 F2 U R2 U2 (17f*)
26. (18f+18b+18d)
    Fa' D B' F2 U F2 L' F' U L' U2 B2 F R' (15f*,19q*)
27. (18f+9b'+18b+18d)
    F2 Ua F2 L2 U R' B U' B2 U B' L2 R U2 (15f*)
28. (18f+9f'+18b+18d)
    B L' U Rs2 D' L2 R D2 R D' F' D2 B' U2 F' L' (17f*)
29. (18f+9b'+9f'+18b+18d)
    D2 R' U R U' L U L' D F2 U2 F' L2 F2 Us' R' U' (18f*)
30. (18f+18b'+18d)
    R2 D2 B2 Us B2 D L' F U' F2 U F' L R2 U2 (16f*)
31. (18f+9b'+18b'+18d)
    R2 Ua' L2 F2 D' U2 F' L D' L2 D L' F' Rs2 U2 (17f*)
32. (18f+9f'+18b'+18d)
    L B R U2 B2 R' F D F' D2 B2 R U B' Ra U' R U (19f*)
33. (18f+9b'+9f'+18b'+18d)
    R2 F' D2 L D' B U D L' F2 D L D' R2 L B U2 R (18f*)
34. (18f+18b+18b'+18d)
    R2 D2 R2 U B2 Us' B2 L' U' F R2 F' U L U2 (16f*)
35. (18f+9b'+18b+18b'+18d)
    F2 Ua Rs2 B2 L2 D R' F D' F2 D F' R' U2 (16f*)
36. (18f+9f'+18b+18b'+18d)
    L2 D' F D' F L D' R D R' U R2 L B' L D F2 L (18f*)
37. (18f+9b'+9f'+18b+18b'+18d)
    B' L U' B2 R Ua' R B R L2 U R' F2 L' U (16f*)
38. (18f+18d')
    F U2 L2 F U2 R D R B' R U' R U' R2 B2 R2 F2 U' (18f*)
39. (18f+9b'+18d')
    F R2 B2 R U' R F2 R2 Fa U R2 U' F' D' Rs2 U (18f*)
40. (18f+9f'+18d')
    Ra U2 L B R2 F D B' F2 U' F2 Us2 F' U R' (17f*)
41. (18f+9b'+9f'+18d')
    Rs2 U2 F R' F2 L' Ua L' B D2 B U' L U F U (18f*)
42. (18f+18b+18d')
    B2 L2 B' Us' R2 F' D' L D2 F D' L F L Us R2 (18f*)
43. (18f+9b'+18b+18d')
    F R D' Rs D' L U' F U2 F D L U' F2 R2 F U' (18f*)
44. (18f+9f'+18b+18d')
    F2 Us' B' L F Ua L F' D2 R L2 B' R2 U' B' U' R (19f*)
45. (18f+9b'+9f'+18b+18d')
    R' D' R' B' R2 D2 B R F U' L2 U2 F U L' U R U2 (18f*)
46. (18f+18b'+18d')
    U' L2 B R B D B' U L2 D' L' U' R U' L U R2 U (18f*)
47. (18f+9b'+18b'+18d')
    R D' F L2 B' U B L2 B2 U F L' D Fs2 U2 R2 U (18f*)
48. (18f+9f'+18b'+18d')
    F2 L2 D' F' D R U' B2 D2 F2 D L2 F2 R2 F' U' R' (17f*)
49. (18f+9b'+9f'+18b'+18d')
    L2 U' L2 U2 L F' U L' B2 D' L' D U B U B2 U F (18f*)
50. (18f+18b+18b'+18d')
    B2 R' D L U2 R2 L Fa D B D' F' B2 D' L2 U R (18f*)
51. (18f+9b'+18b+18b'+18d')
    L B' L2 U2 L2 U F2 U D2 B R B2 R2 D R F2 U' (17f*)
52. (18f+9f'+18b+18b'+18d')
    B L' F U2 D' R Ua B2 R D B R2 F D' R' D' L (18f*)
53. (18f+9b'+9f'+18b+18b'+18d')
    Ra' B2 R2 F' R2 Ua' B' R' B U2 F' L B U2 B2 (17f*)
54. (18f+18d+18d')
    B2 U2 L2 D' B D' L D2 L' U' B2 Ua B' U L2 B2 U (18f*)
55. (18f+9b'+18d+18d')
    L U' B Us2 L' U D2 L U' B2 R' U B R U2 D B' (18f*)
56. (18f+9f'+18d+18d')
    B U2 B2 R L2 B2 U' B L2 U' R U2 R2 U' B R' D F2 U' (19f*)
57. (18f+9b'+9f'+18d+18d')
    B R2 F2 U2 R Us B2 R2 F' Ra D' L' D' L B2 R' U (19f*)
58. (18f+18b+18d+18d')
    B L' U B R2 U D2 B2 L F2 U2 B' R' B D' L2 U' (17f*)
59. (18f+9b'+18b+18d+18d')
    L U L U Rs2 F2 R' F' D' F' L2 F2 L D2 B2 R' U' (18f*)
60. (18f+9f'+18b+18d+18d')
    B' L2 F L U' L B R D R' U2 R2 B D' B2 D' L2 U (18f*)
61. (18f+9b'+9f'+18b+18d+18d')
    L U2 B D' R U2 D' R2 U' B' L2 F B2 D' B2 U2 L U (18f*)
62. (18f+18b'+18d+18d')
    L2 U L2 B2 U' B2 D2 R D F' D2 F D' R U' R2 Ua (18f*)
63. (18f+9b'+18b'+18d+18d')
    L2 D R2 F2 U' F2 D2 L' D' B R2 B' D L' U R2 U2 (17f*)
64. (18f+9f'+18b'+18d+18d')
    B2 D' B2 R F2 D2 L2 D' F U L' F U' F R2 U' R F' U (19f*)
65. (18f+9b'+9f'+18b'+18d+18d')
    L B2 R D2 U2 B' D U2 Ra U Fa' D' F' L U2 R (18f*)
66. (18f+18b+18b'+18d+18d')
    F R F R' F2 R' D' F D2 L2 U' B R D' L2 U R (17f*)
67. (18f+9b'+18b+18b'+18d+18d')
    L2 Us L' D' B' U R2 Us' R B F2 R B L' (16f*,19q*)
68. (18f+9f'+18b+18b'+18d+18d')
    U B2 U2 R2 D' L' D L2 D' R' B' R2 D B U' L B U2 F (19f*)
69. (18f+9b'+9f'+18b+18b'+18d+18d')
    B R2 D' R' B2 L2 B2 D2 F2 B R2 U' L' D B2 U2 F U (18f*)

Now consider all patterns without 18f. There are quite a few that mix the F and R colours, and the B and L colours.

70. (18b+9f)
    Us R2 Ds L Ds F R2 F' Us L' B2 R2 (16f*)
71. (18c+9f)
    D2 L' F L2 U R' Fs2 L' R2 U' R2 B' R U2 (15f*)
    F D U' R B' R' D L' D L B' U' B U' F L' D U' (18q*)
72. (18d+9f)
    B2 D B2 L U2 L F2 U R U F U' F' L2 R' (15f*)
    R' F' D U2 B D U' L' D L F' L D U' F' R2 (18q*)
73. (18b+9b')
    D' F2 D (F2 R2)³ U F2 U' (12f*)
    F D' U F D' U' F U F' D U' F D U F' U' (16q*)
74. (18c+9b')
    U F2 Ua' F2 D (6f*,8q*)
75. (18d+9b')
    (F2 R2)³ D' F2 Ua F2 U' (12f*)
76. (18b+9c)
    B2 R2 B2 D' U2 R2 D' R2 B2 R2 D2 U' B2 U' (14f*)
77. (18c+9c)
    U B Ra F2 Ra' B' U' (9f*,10q*)
78. (18d+9c)
    U' L2 F2 D2 R2 D Rs2 U B2 U2 R2 B2 U' (14f*)
79. (18b+9f+9b')
    B' R' B' U R D' F L2 R D F' R' F' R F R U' (17f*,18q*)
80. (18c+9f+9b')
    U F2 D2 L2 D2 U' F2 R Us F' L2 F Ds R' (16f*)
81. (18d+9f+9b')
    U' B2 U2 F2 L2 B2 U' B F2 D' B R' U2 B' U B' R' (17f*)
82. (18b+9b'+9c)
    R2 D' U2 Fs2 L2 Fs2 L2 U' L2 Ds (13f*)
83. (18c+9b'+9c)
    D2 L2 F2 U' Fs2 D' U2 B2 L2 Ua' (12f*)
84. (18d+9b'+9c)
    D' R2 F2 U2 F2 D' Rs2 D' F2 U2 F2 L2 U' (14f*)
85. (18b+9c+9f')
    L2 F2 L' U B2 U' B R2 B' U B2 U' L' (13f*,18q*)
86. (18c+9c+9f')
    U R2 Ua' B2 L2 U' L B D Rs2 U' F' L' (15f*)
87. (18d+9c+9f')
    L B L' Fa D2 F' D B' L Fa' U2 F U' L' (16f*,18q*)
88. (18b+9b'+9c+9f')
    F2 U' Fs2 R2 B2 R' Us F L2 F' Ds R' U R2 (17f*)
89. (18c+9b'+9c+9f')
    U' L2 F2 D2 L' Fs D' L2 D F2 R2 Fa L' U' (16f*)
90. (18d+9b'+9c+9f')
    B R2 B2 L U B2 U Fs2 U' L2 D' B L2 F2 L' R2 (17f*)
91. 2X, adjacent 2H (18b+18c')
    F2 D' R2 F2 L2 U' R2 D' L2 F2 R2 U' (12f*)
92. (18b+18d')
    U B2 D Rs2 Us' Rs2 U' B2 U' (12f*)
93. (18c+18d')
    L2 D' Fs2 Ua Fs2 U' L2 (10f*,16q*)
94. 2X, adjacent 2A, adjacent 2K (18b+18c'+9f)
    B' R U R' U' B' Rs2 D' R2 B F2 U2 B' L2 U' R2 (17f*)
95. (18b+18d'+9f)
    B F2 L D L' D' B' R2 D' L2 F' D2 F' R2 U' F2 R2 (17f*)
96. (18c+18d'+9f)
    B2 D Rs2 D2 F2 D F2 U' L2 U B2 L F U' F2 U F' L'
97. (18b+18c'+9c)
    D' F2 L2 D2 F2 U' Rs2 U' B2 U2 R2 F2 U' (14f*)
98. (18b+18d'+9c)
    U2 Rs Us2 Rs' U B2 Ua' F2 U' (13f*)
99. 2W, 4T (18c+18d'+9c)
    D Rs' F2 Ua L' Us' Rs D' F2 U' (14f*)
100. (18b+18c'+9c+9f)
     U' B2 D2 B2 R2 F2 U' F2 B D' B R' U2 B' U B' R' (17f*)
101. (18b+18d'+9c+9f)
     U F2 U2 R2 D' F2 R Fs' U' B2 D2 U' Fs' L' U2 (17f*)
102. 2W, 4ct (18c+18d'+9c+9f)
     D B2 U' L2 F R' U' Rs2 D R B L2 U L2 U' (16f*)
103. (18b+18c'+9b')
     D' B2 D F2 R2 F2 R2 F2 R2 U B2 U' (12f*)
104. (18b+18d'+9b')
     D2 Rs2 F2 Us R2 D L2 U2 B2 U' (12f*)
105. (18c+18d'+9b')
     D2 Rs' F Ra Ua Ra F Rs' U2 (14f*,16q*)
106. 2V, 2Y, 2 diag (18b+18c'+9b'+9f)
     D F2 U R2 F' L D Fs2 U' R' F' L2 U' R2 U' (16f*)
107. (18b+18d'+9b'+9f)
     D' B2 D2 L2 D F2 R' Us' B L2 B' Us L2 R' U2 (17f*)
108. (18c+18d'+9b'+9f)
     D' L U' B' L' F' Ra U' R B L' U2 L2 F U' (16f*)
109. 2O, 2I, 2+ (18b+18c'+9b'+9c)
     D' L2 D2 F2 U' Rs2 U' B2 U2 R2 U' (12f*)
110. (18b+18d'+9b'+9c)
     U F2 D R2 Fs2 U2 Fs2 U2 R2 U' F2 U' (14f*)
111. (18c+18d'+9b'+9c)
     U L2 U2 F2 U' Rs2 D B2 U2 R2 U' (12f*)
112. 2O, 2U, 2t (18b+18c'+9b'+9c+9f)
     D B' D' L' Fs2 R U F' L' Us' F Ra U' (16f*,18q*)
113. (18b+18d'+9b'+9c+9f)
     D2 R2 B2 D' Rs2 D R Fs' U F2 U' Fs L2 R' U2(17f*)
114. (18c+18d'+9b'+9c+9f)
     R2 F2 Us L' Us' B D2 F2 U2 B' Us' R' (15f*)

There are also several that mix the F and L colours, and the B and R colours.

115. (18b+9b+9c'+9d'+9f')
     L2 B2 Us L Ds B' D2 B2 U2 B' Us L' (15f*)
116. (18b+9b+9c'+9d')
     D' L2 U2 B2 D F2 B2 D F2 U2 L2 U' (12f*)
117. (18b+9b+9c'+9f')
     F' L2 B2 L U' F2 Us R2 D F' D' F2 L2 B2 U' L' (17f*)
118. (18b+9b+9c')
     D' R2 D2 B2 D Rs2 D F2 U2 L2 U' (12f*)
119. (18b+9b+9d'+9f')
     D L2 D' F2 R2 F2 D2 U' F' L D Fs2 U' R' F' U' (17f*)
120. (18b+9b+9d')
     D2 B2 L2 D Rs2 D' B2 R2 D B2 U2 R2 U' (14f*)
121. (18b+9b+9f')
     B2 R2 Ua' B' L' B2 R U B' D' B' U R D2 L' F U' (18f*)
122. (18b+9b)
     B2 R2 B2 D B2 D' L2 F2 L2 U R2 U' (12f*)
123. (18b+9c'+9d'+9f')
     D L2 U' L2 B2 L2 D F' L D Fs2 U' R' F' U' (16f*)
124. (18b+9c'+9d')
     D L2 U' L2 B2 L' D2 Fs2 U2 R' U F2 U' (14f*)
125. (18b+9c'+9f')
     R2 F2 R' F U2 F' U R2 U' F U2 F' R' (13f*)
126. (18b+9c')
     F2 R2 F2 D' U2 F2 D' L2 B2 L2 D2 U' R2 U' (14f*)
127. (18b+9d'+9f')
     B2 U' B2 U' F2 R2 Ds F R2 D' F L B' D' B' L' (17f*)
128. (18b+9d')
     Fs2 R2 U' Rs2 D2 Fs2 U' R2 (11f*)
129. (18b+9f')
     L' B' L' B' L R2 B2 L2 B' F D' B D F L' (15f*)

Let's now consider patterns which use only opposing colours. The pattern must use 18b on one edge orbit only. The corners can only move by 5a, 9a or 9a'.

130. (18b+5i)
     L2 F2 L2 Us R2 F2 R2 Us' (10f*)
     L2 B2 (Us2 L2 F2)² (10f*)
131. (18b+5g)
     (R2 Us R2 F2)² (10f*)
     U2 Rs2 Fs2 U2 (R2 B2)² L2 B2
132. (18b+5g+5i)
     R2 F2 L2 Us2 F2 L2 B2 (8f*)
133. (18b+9a)
     B2 U2 F2 R2 U2 R2 F2 U2 B2 (9f*)
134. (18b+9a+5i)
     B2 U2 F2 R2 D2 L2 B2 D2 B2 (9f*)
135. (18b+9a+5g)
     Us2 R2 U2 R2 F2 U2 F2 R2 U2 R2 (11f*)
136. (18b+9a+5g+5i)
     Us2 R2 U2 R2 F2 D2 B2 L2 D2 R2 (11f*)
137. (18b+9a')
     R2 F2 R2 Us R2 F2 R2 Us' (10f*)
     R2 Us2 F2 R2 F2 R2 Us2 F2
138. (18b+9a'+5i)
     R2 F2 R2 B2 R2 B2 (6f*,12q*)
139. (18b+9a'+5g)
     Us2 (F2 R2)³ (8f*)
140. [p49] (18b+9a'+5g+5i)
     R2 Us L2 B2 L2 Us L2 F2 (10f*)
     (B2 R2 Us2)² F2 R2 Us2
141. (18b+5a)
     R2 U2 R2 F2 U2 F2 R2 U2 R2 (9f*)
142. (18b+5a+5i)
     R2 U2 R2 F2 D2 B2 L2 D2 R2 (9f*)
143. (18b+5a+5g)
     Us2 L2 U2 L2 B2 D2 B2 L2 U2 L2 (11f*)
144. (18b+5a+5g+5i)
     Us2 B2 U2 B2 L2 U2 R2 F2 D2 B2 (11f*)

There is one type of pattern that I had almost overlooked, which uses both adjacent and opposing colours on the four sides. Such a pattern involves only edges.

145. 4H of order 4, type 2 (9d'+18d)
     Fs2 U2 B2 R2 D' Rs2 U L2 F2 D2 (12f*)
     L' B R U' B L' D' B F U' R' F D' L F R' (16q*)
146. 4H + 2 fish, type 1 (9d'+18d+18b)
     Rs' Us L' Fs2 R Us' Rs' (12f*,14q*)
147. 4H + 2 fish, type 2 (9d'+18d+18b')
     D' L2 B2 L2 Ua' R2 F2 R2 U' (10f*)
     U B2 Ra' Ua B2 Ua Ra' U' (14q*)
148. 4H + 2X (9d'+18d+18b+18b')
     L2 F2 L2 U' L2 D R2 B2 R2 D F2 U' (10f*)
     Rs' Us L Fs2 R' Us' Rs' (14q*)

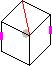
19. Symmetry m_er2_e, <(24), i>, 4.

Suppose the r2 symmetry is centred around the FL/BR middle layer edges, and that a plane of reflectional m symmetry is perpendicular to the r2 axis.

The corners lie in 3 orbits. The 4 corners not in the m plane, i.e. {UFL,DFL,UBR,DBR}, form one orbit and they can move only by 9a'-c' and twisted by the following:

1. 4-twist of corners, type 2 {UFL+,DFL+,UBR-,DBR-}
   R' B' U2 B R2 D2 F' R D2 R U2 B' L2 R U2 (15f*)

The opposite pairs of the other corners can be swapped separately if an odd permutation of edges can be found. The pairs can also be interchanged using 9a-c as before. They cannot be twisted.

The U/D edges also occur in two orbits of 4 edges, different to those in section 17, viz. {UL,UB,DF,DR} {UF,UR,DB,DL}. They can be moved in similar ways by double swaps:

2. 2-swap of edges, type 7 (UL,DR)(UB,DF)
   U2 (F2 R2)³ U2 (8f*)
3. 2-swap of edges, type 8 (UL,DF)(UB,DR)
   U' R2 F2 R2 U2 F2 R2 F2 U' (9f*)
4. 2-swap of edges, type 9 (UL,UB)(DF,DR)
   Rs' Us' L Us B2 Rs D (11f*,10q*)

The two orbits can be swapped, by 5g or 9d' for example. They can be flipped too:

5. 4-flip of edges, type 2 {UL+,UB+,DF+,DR+}
   U2 R F2 R2 F R2 F2 R' U2 B2 L2 D L2 B2 (14f*)

Not only can the middle edges move the same as section 9, i.e. opposite swaps with 5i, and flipped in pairs by 9f, this time a single swap of the middle edges is possible because it can be combined with the single swap of corners.

6. Corner swap and edge swap type 1 [p142] (LB,RF)(DBL,UFR)
   R U' R' B R U R2 B' D B D' B R B' (14f*,15q*)

These patterns form a group of order 98,304 (= 2¹⁵3).

This group has many nice patterns. There are several that look like they have r3 symmetry, but do not because exactly one pair of opposite faces have their two colours mixed.

Here are the patterns involving 19f:

7. (19f+9f')
   F2 U F2 L2 D Fa L' U2 F2 R' Ua F Ra' (16f*)
8. (19f+19c)
   R2 U' B2 D' B2 U2 R2 U' F' R' F2 L D' L F' D R (17f*)
9. (19f+9f'+19c)
   L2 B2 D U2 F2 D Fa L2 R D2 B2 R' Ua F Ra' (18f*)
10. Tripod type 2 [p117, RCC 3.9.36] (19f+19c')
    F2 R2 D R2 Ua F2 D' R' D' F L2 F' D R U' (16f*)
11. (19f+9f'+19c')
    B2 D R2 U' L2 F2 R2 Fa' R' D2 B2 R' Ua F Ra' (18f*)
12. (19f+19c+19c')
    R F R2 U2 F D' L' B' U2 F U' Rs2 D F U' F U (18f*)
13. (19f+9f'+19c+19c')
    L' B R' U B' U2 B Rs' B' U F2 U2 D R2 L U' F2 (18f*)
14. (19f+9c')
    F Ua L' D L' D F L2 D' F' L2 D2 L' D2 L U' (17f*)
15. (19f+9c'+9f')
    F L D' L2 D Rs U' R2 F R2 B' D R' F2 B U (17f*)
16. Duck feet type 2 (19f+9c'+19c)
    D' F' R2 F U R' D' B2 D2 F R2 F' U' B2 R' B (16f*, 21q*)
    D2 B2 D' R2 U2 F2 U R2 B2 D' R F' U F2 U' F L2 R'
17. (19f+9c'+9f'+19c)
    B2 R' B2 U' B D L U B2 D' B R2 U' F2 U R' (16f*)
18. [p119] (19f+9c'+19c')
    L2 Us2 L F' D F2 D' F L' U F2 U2 F2 D2 L2 (16f*)
    R2 U2 B2 D2 B2 D R' B U' B2 U B' R Us2 R2
19. (19f+9c'+9f'+19c')
    F R U' L D2 U' R D F' R F' R2 U' R' F' L U' (17f*,19q*)
20. (19f+9c'+19c+19c')
    R' F' L2 B F2 R2 F' U R' F' L2 U F' D U2 F2 U' (17f*)
21. Cherries / Chickenfeet, type 2 [p68] (19f+19c+19c'+9c'+9f')
    F' L U B L' F' D' F U F' L2 B R D' L2 U F' (17f*, 19q*)
22. (19f+9d)
    Rs2 B2 U' L2 F2 U B D R' D2 R D' B L2 U' B2 U2 (18f*)
23. (19f+9d+9f')
    B2 U2 D2 R' U L' B Rs D' L2 F R' B' U R D' L U (19f*)
24. (19f+9d+19c)
    U2 L2 U' B2 D2 L2 U R2 F2 D R' B U' B2 U B' R' (17f*)
25. (19f+9d+9f'+19c)
    B D2 Rs2 F2 B L D' B D2 L U' F' D R' D2 L2 U' (18f*)
26. (19f+9d+19c')
    R B U' B2 U B' R D' F2 R2 U' L2 D2 B2 U L2 U2 (17f*)
27. (19f+9d+9f'+19c')
    L2 B2 U' L2 D Ra' B Us' R2 B2 L D2 Fa D R2 (18f*)
28. (19f+9d+19c+19c')
    B L' F D' B Rs2 U2 B' Rs2 D R D L U2 R (17f*)
29. (19f+9d+9f'+19c+19c')
    L' B' D L2 D2 R2 B R2 B2 D R2 F2 R2 B L F2 R2 F2 (18f*)
30. (19f+9d+9c')
    R2 U' F2 U' R2 U' R2 F2 L2 R D B' L2 B D' L2 R D2 (18f*)
31. (19f+9d+9c'+9f')
    Fa D2 L Us B' U2 R F' L F2 R' F R' D' L2 F2 (18f*)
32. (19f+9d+9c'+19c)
    L2 D2 B2 D' R F2 U' B' R2 B' F2 D' B2 L2 R' F2 R2 (17f*)
33. (19f+9d+9c'+9f'+19c)
    B2 Ra' U2 R' D' B' U' Rs2 D L2 B2 D' L' D F (17f*)
34. (19f+9d+9c'+19c')
    L2 B2 L' R2 F2 U' B2 F' L2 F' D' B2 L U' F2 U2 R2 (17f*)
35. (19f+9d+9c'+9f'+19c')
    L' U' F U R2 F2 U' Fs2 D R U B D2 Fa R2 (17f*)
36. (19f+9d+9c'+19c+19c')
    F U2 B2 D2 R' U R2 U R2 U' F2 U B2 U L2 U2 L' F' (18f*)
37. (19f+9d+19c+19c'+9c'+9f')
    F2 R2 F' D L B2 L' D' R' D2 B2 U' R F2 L' D' F' (17f*)

Here are those not involving 19f, but which still mix the F and L colours as well as the R and B colours.

38. (19c+9b)
    D F Ra' B2 Ra F' D' (9f*,10q*)
39. (19c+9c')
    D U2 R2 Ua' R2 U' (7f*,10q*)
40. (19c+9b+9c')
    B2 R2 D' Rs2 U' D2 L2 B2 Us (11f*,18q*)
41. Hexagon (19c+9f')
    U B2 U' F' Us' L' D2 L Us F D' L2 B2 D' (16f*, 20q*)
42. (19c+9b+9f')
    U F2 Ua L2 B2 U' R B U Rs2 D' F' R' (15f*)
43. (19c+9c'+9f')
    D B2 D2 L2 D B2 R Us' B' L2 B Us R' (15f*)
44. Cube within cube within cube, type 3; exchanged rings [RCC 3.9.35] (19c+9b+9c'+9f')
    F Us L' B2 L Us' F U Rs2 U' L2 F2 (15f*)
    D' L2 U L D L' U' B' D2 U' B' D' L B U B (18q*)
45. (9d+19c)
    R2 B2 U' R2 B2 F2 R2 U L2 R2 F2 R2 (12f*)
46. (9d+19c+9b)
    B2 F2 U2 R2 B2 F2 R2 U L2 D U R2 U' (13f*)
47. (9d+19c+9c')
    U2 R2 D U' F2 L2 R2 D B2 U2 L2 U' (12f*)
48. (9d+19c+9b+9c')
    U R2 U F2 D2 U2 F2 L2 R2 U' L2 U' (12f*)
49. (9d+19c+9f')
    Rs2 D2 F2 L B2 D R2 F2 L2 R' F R B2 D R F U2 (18f*)
50. (9d+19c+9b+9f')
    D2 F Rs D2 U L2 U L' R B' R2 D B2 D2 R2 U' (17f*)
51. (9d+19c+9c'+9f')
    F2 L2 U B' R D' R2 D B' L2 B R' B U' B2 R2 (16f*)
52. (9d+19c+9b+9c'+9f')
    L2 R F2 R2 B R2 D' F2 R' F2 D2 R2 B F2 R2 D' R2 (17f*)

These patterns mix F and R colours, and B and L colours.

53. (19d+5f)
    R2 B2 U R2 Fs2 R2 U' Rs2 F2 R2 (12f*)
54. (19d+9b')
    U' F2 U2 R2 U F2 U2 R2 F2 Rs' F2 Ra' (14f*)
55. (19d+5f+9b')
    L2 F2 U' F2 D' B2 D' B2 L2 U F2 U' F2 U' (14f*)
56. (19d+9c)
    U2 Rs2 D' F2 Ua F2 U' Rs2 U2 (12f*)
57. (19d+5f+9c)
    D2 L2 R2 U' L2 D U L2 U' L2 R2 D' U' (13f*)
58. (19d+9b'+9c)
    D' F2 U2 R2 D Rs2 D L2 U2 F2 U' (12f*)
59. (19d+5f+9b'+9c)
    F2 L2 U' Rs2 D' U2 R2 F2 Us' (11f*)
60. (19d+9f)
    L U' L' B D B' U2 R2 D R D R' B D2 R2 U' (16f*)
61. (19d+5f+9f)
    B2 R2 F R2 D R2 B2 F' R2 B L2 R F' D' F' L2 R U' (18f*)
62. (19d+9b'+9f)
    Ua R' U R F' U' F' L' D L' F L2 F R' Ua' (17f*)
63. (19d+5f+9b'+9f)
    D F2 D L2 F2 L2 U' L F' D' Rs2 U B L' R2 U' (17f*)
64. (19d+9c+9f)
    B2 R2 U L' B L' F2 L D' B2 D B' L U' B2 R2 (16f*)
65. (19d+5f+9c+9f)
    U' R' F' L U L F R2 B2 L F U F L' B' U' (16f*)
66. (19d+9b'+9c+9f)
    L' F2 Us2 R2 F' R2 D B2 R B2 U2 L2 B' R2 U' R2 (17f*)
67. (19d+5f+9b'+9c+9f)
    L2 F2 U' Rs2 U R' Fs' U' B2 U Fs R' (15f*)

Finally, those patterns that only mix opposing colours.

68. (19b+9a)
    R2 D2 F2 U2 F2 Rs' B2 Ra' (10f*)
    (D2 R2)² F2 U2 F2 (R2 D2)²
69. (19b+9a')
    R2 U2 F2 U2 F2 Rs' F2 Ra' (10f*)
    (U2 F2)² R2 U2 R2 (F2 U2)²
70. (19b+9a+9a')
    B2 L2 B2 Ua F2 R2 F2 Us' (10f*)
    Fs2 U2 (R2 F2)² L2 F2 D2 Rs2
71. (19b+5i)
    U2 R2 F2 R2 Ds R2 B2 R2 Ua' (11f*)
    Fs2 Rs2 U2 (R2 F2)³ D2
72. (19b+9a+5i)
    R2 U2 B2 D2 F2 Rs' B2 Ra' (10f*)
    (U2 L2)² B2 U2 F2 R2 D2 L2 U2
73. (19b+9a'+5i)
    R2 D2 B2 D2 F2 Rs' F2 Ra' (10f*)
    (U2 F2)² R2 D2 L2 B2 D2 F2 U2
74. (19b+9a+9a'+5i)
    U2 F2 R2 (F2 L2)² U2 (8f*)
75. (19b+5f)
    D2 L2 F2 L2 Us' R2 B2 R2 Ua' (11f*)
    Rs2 Fs2 D2 F2 R2 (F2 L2)² D2
76. (19b+9a+5f)
    D2 R2 U2 R2 F2 U2 F2 R2 U2 R2 U2 (11f*)
77. (19b+9a'+5f)
    D2 L2 U2 R2 F2 U2 F2 R2 U2 L2 U2 (11f*)
78. (19b+9a+9a'+5f)
    D2 (F2 R2)³ U2 (8f*)
79. (19b+5i+5f)
    D2 (B2 R2)²F2 R2 U2 (8f*)
80. (19b+9a+5i+5f)
    D2 R2 D2 L2 B2 D2 F2 (R2 U2)² (11f*)
81. (19b+9a'+5i+5f)
    (D2 L2)² B2 D2 F2 R2 U2 L2 U2 (11f*)
82. (19b+9a+9a'+5i+5f)
    R2 F2 U L2 Fs2 R2 D' F2 R2 (10f*)
    Fs2 Rs2 D2 (F2 R2)³ D2

20. Symmetry m_cr2_f, <(13)(24), i>, 4.

Hold the cube so that the r2 symmetry is centred around the U/D faces. Note that the m_f symmetry through the middle layer also lies in this group. The patterns of this group also includes those of sections 9, 11, and 13.

The corners are in two orbits; the {URF,UBR,DFR,DRB} corners form one set, the remaining ones the other. Each orbit can move in the usual three ways by using 9a-c, and swapped by 13a for example, and twisted by the following:

1. 4-twist of corners, type 3 {UBR+,UFL+,DBR-,DLF-}
   Ra D Ra' U F2 L' Ua' R' Ua L F2 U' (16f*)

The edges lie in 4 orbits; each vertical slice forms one orbit and the pairs of opposite edges in the middle slice form the other two orbits. The edges in a vertical slice can be moved in three ways by using 11b (the 2H pattern) in different orientations, or 5d to flip them. Those two orbits can be swapped by using for example 9d or 13c.

The edges in the middle layer move the same as section 9, i.e. opposite swaps with 5i, and flipped in pairs by 9f. A single swap within one orbit is not possible because there is no other odd permutation to accompany it.

These patterns form a group of order 589,824 (= 2¹⁶3²).

Suppose we have a 4-cycle of colours on the sides, for example by using 13a or 13c. By combining this with the 2H pattern 11b to break the extra symmetries, we find the following patterns:

2. 6H of order 4, type 1 (13c+11b)
   U R2 Fs2 R2 Fs2 D' Rs2 (10f*)
3. 2H + 4+ of order 4 (13a+11b)
   Fs2 U' F2 Rs2 F2 Rs2 U (10f*)
4. 2H, 4I (13a+13c+11b)
   Fs2 L2 Fs2 R2 Us (8f*)
   Ua Rs Fs2 Rs' U2 (12q*)

We could also swap adjacent colours on the sides by using 9b and/or 9c' on the corners, 9d and/or 9f on the edges and again combining it with 11b on one edge orbit to spoil the unwanted r2_e symmetries.

5. 6H of order 4, type 2 (9d+11b)
   U Rs2 D2 Fs2 U R2 Fs2 R2 (11f*)
6. 2H, 4A (9f+11b)
   R2 D2 B2 D2 R Fs D L2 F2 R2 U Fs R' (15f*)
7. 2H, 4K (9d+9f+11b)
   B2 U' L2 B2 L' F D F' Rs2 U' L' F2 U' B2 R' U2 R' (18f*)
8. 2S, 4a (9b'+11b)
   R2 F2 R2 D R2 D' L2 B2 L2 U F2 U' (12f*)
9. 2S, 4a (9c+11b)
   R2 L2 D' B2 D2 L2 B2 D2 R2 F2 U2 L2 U' (13f*)
10. 2I, 4+ (9b'+9c+11b)
    D2 R2 L2 D' B2 U2 R2 L2 U2 F2 U' (11f*)
11. 2S, 4T (9b'+11b+9d)
    L2 R2 D' F2 D2 L2 B2 U2 R2 B2 D2 R2 U' (13f*)
12. 2S, 4T (9c+11b+9d)
    L2 R2 D' B2 D2 L2 F2 U2 R2 F2 D2 R2 U' (13f*)
13. 6I (9b'+9c+11b+9d)
    U2 R2 D2 U2 R2 D' U' (7f*,12q*)
14. 2S, 4Y (9b'+11b+9f)
    R2 D2 R2 D' R2 U' F2 U L2 F' D' R D2 R' D B2 F' U (18f*)
15. 2S, 4 rectangle (9c+11b+9f)
    L2 F2 L2 . R F R2 B' D B2 D' B R2 F' R' (14f*)
16. 2I, 4t (9b'+9c+11b+9f)
    F L2 F2 R' D' F2 Us' L2 U F' D' L2 F2 R2 U' R' (17f*)
17. 2S, 4V (9b'+11b+9d+9f)
    L2 U L' U L D' B2 D' R2 D' B L' U' L B F2 U2 (17f*)
18. 2S, 4ct [p158] (9c+11b+9d+9f)
    D' R2 U F2 L B' D' Fs2 U B R F2 U' F2 U (16f*)
19. 2I, 4U (9b'+9c+11b+9d+9f)
    B2 L2 D U' B' L' R D' R2 D' U2 L' R F' (14f*)

All remaining patterns use opposing colours, and are in fact in the square group. First I'll list the patterns that move the corners by 13h = 13a+5b. To spoil the r4 symmetry we can move the middle layer by 11b', or move the other two edge orbits differently from each other. This leads to 4*4+2*6=28 more nice patterns:

20. 2+ 2c 2a
    B2 R' F2 L2 Fs2 L2 F2 R' F2 (10f*)
    (L2 F2 U2)² F2 L2 U2 (R2 F2)²
21. 2I 2c 2a
    B2 L Us2 R2 Us2 L' F2(9f*)
    (L2 F2 U2)² F2 L2 U2 L2 D2 L2 F2
22. 2+ 2D 2a
    F2 L2 Ua B2 R2 Ua B2 R2 U2 (10f*)
    (L2 F2 U2)² F2 R2 D2 L2 F2 R2 F2
23. 2I 2D 2a
    B2 R' Ua Rs2 Ua' R' F2 (10f*)
    (L2 F2 U2)² B2 L2 U2 (L2 F2)²
24. 2I 2c 2a
    Us2 R2 B' L2 Us2 R2 F' R2 (10f*)
    (L2 F2 U2)² F2 L2 U2 R2 B2 L2 B2
25. 2O 2c 2a [p85]
    L2 F Rs2 B2 Rs2 F' R2 (9f*)
    (L2 F2 U2)² B2 R2 D2 (R2 B2)²
26. 2I 2D 2a
    R2 B' D2 Rs2 U2 F' R2 (8f*)
    (L2 F2 U2)² F2 R2 D2 (L2 B2)²
27. 2O 2D 2a
    L2 F2 Rs2 B D2 Rs2 U2 F' R2 (11f*)
    (L2 F2 U2)² F2 R2 D2 R2 F2 R2 B2
28. 2+ 2c 2T
    B2 L2 Ua F2 R2 Ua F2 R2 U2 (11f*)
    (F2 L2 U2)² R2 F2 U2 B2 L2 B2 R2
29. 2I 2c 2T
    L2 B' D2 F2 Us2 F2 D2 B' R2 (10f*)
    (F2 L2 U2)² L2 B2 D2 (F2 L2)²
30. 2+ 2D 2T [p133]
    L2 B F2 L2 Us2 R2 F' R2 Fs2 (11f*)
    (F2 L2 U2)² R2 F2 Rs2 D2 (F2 L2)² (antipode in square group)
31. 2I 2D 2T
    F2 L2 Ua F2 L2 Ua F2 R2 U2 (11f*)
    F2 (U2 R2)³ B2 D2 R2 F2 R2 U2
32. 2I 2c 2T
    Us2 R2 F' D2 Rs2 U2 B' R2 (10f*)
    (F2 L2 U2)² R2 F2 U2 (F2 R2)²
33. 2O 2c 2T [p84]
    F2 R2 L U2 Fs2 D2 R' F2 (9f*)
    (F2 L2 U2)² R2 F2 U2 F2 L2 B2 L2
34. 2I 2D 2T
    R2 F R2 Us2 L2 B R2 (8f*)
    R2 (U2 F2)³ L2 U2 F2 L2 F2 D2
35. 2O 2D 2T
    F2 L2 R B2 Us2 F2 L' F2 (9f*)
    R2 (U2 F2)³ R2 D2 B2 R2 F2 D2
36. 2I 4a
    B2 Us2 R' B2 Us2 F2 L' F2 (10f*)
    F2 (U2 R2)² D2 L2 F2 U2 L2 F2 L2 D2
37. 2+ 2T 2a
    B2 R2 Ua B2 R2 Ua' B2 R2 U2 (11f*)
    R2 (U2 F2)² (D2 B2 R2)² B2 D2
38. 2I 2T 2a
    B2 Us2 L' D2 Fs2 U2 R' F2 (10f*)
    (F2 R2 U2)² R2 B2 U2 (B2 L2)²
39. 2I 2T 2a
    F2 L2 Ua B2 L2 Ua' F2 R2 U2 (11f*)
    F2 (U2 R2)² (D2 R2 F2)² R2 U2
40. 2O 2T 2a
    Ra U2 Fa U2 Fa Ra' U2 (11f*)
    (F2 R2 U2)² R2 B2 U2 F2 R2 F2 L2
41. 2I 4T
    B2 R2 Ua F2 L2 Ua' F2 R2 U2 (11f*)
    (F2 R2 U2)² R2 F2 D2 F2 L2 B2 L2
42. 2I 4c
    F2 R2 Ua' F2 R2 Ua B2 R2 U2 (11f*)
    B2 (U2 R2)² (D2 R2 F2)² L2 D2
43. 2+ 2D 2c
    B2 R2 Ua' F2 L2 Ua B2 R2 U2 (11f*)
    R2 (F2 D2)² F2 U2 R2 D2 F2 L2 F2 D2
44. 2I 2D 2c
    R2 B2 Ua' R2 F2 Ua R2 F2 U2 (11f*)
    R2 (F2 U2)² F2 D2 L2 U2 F2 L2 B2 D2
45. 2I 2D 2c
    F2 L2 Ua' F2 R2 Ua F2 R2 U2 (11f*)
    F2 (R2 U2)² L2 U2 F2 U2 R2 F2 R2 D2
46. 2O 2D 2c
    Ra U2 Fa' D2 Fa' Ra' U2 (11f*)
    L2 B2 L2 (F2 R2 D2)² L2 F2 U2 B2
47. 2I 4D
    B2 R2 Ua' B2 R2 Ua F2 R2 U2 (11f*)
    R2 D2 L2 F2 (U2 F2 L2)² F2 L2 B2

Next suppose the corners move using 9a. To break the r2_e symmetry, either the middle layer edges are moved by 11b', or the other two edge orbits move differently. As the faces show opposing colours, the edge orbits are not be swapped. This leads to a further 28 patterns.

48. 4T + 2H (9a+11d')
    R2 F2 Ua L2 B2 Ua L2 F2 U2 (11f*)
    D2 F2 (D2 R2)³ F2 U2 R2 F2 R2
    R2 U2 B2 D2 F2 (D2 B2 L2)² F2 D2
49. 2c + 2a
    R2 Us2 F' L2 Us2 R2 B' R2 (10f*)
    F2 (U2 R2)² (D2 R2 F2)² L2 D2
50. 2H + 2c + 2a, type 1
    Ra' Fa U2 Fa U2 Ra' U2 (11f*)
    L2 (U2 F2)² D2 F2 R2 U2 F2 R2 F2 D2
51. 2D + 2a
    Fa' D2 R2 F2 U2 L2 Fa' U2 R2 (11f*)
    (F2 R2 U2)² R2 B2 U2 F2 L2 B2 L2
52. 2H + 2D + 2a, type 1
    F2 R2 Ua' F2 L2 Ua B2 R2 U2 (11f*)
    (F2 R2 U2)² R2 B2 U2 (F2 R2)²
53. 2H + 2c + 2a, type 2
    F2 L2 Ua' F2 L2 Ua F2 R2 U2 (11f*)
    F2 (D2 R2)² (U2 L2 F2)² R2 U2
54. 2X + 2c + 2a [p134]
    F2 D2 R2 U' L2 Fs2 R2 D' R2 U2 F2 (12f*)
    (F2 R2 U2)² R2 B2 Rs2 D2 (F2 L2)² (antipode in square group)
55. 2H + 2D + 2a, type 2
    Fa' Ra D2 Ra U2 Fa' U2 (11f*)
    (F2 R2 U2)² L2 F2 D2 (F2 L2)²
56. 2X + 2D + 2a
    B2 L2 Ua' F2 R2 Ua F2 R2 U2 (11f*)
    (F2 R2 U2)² R2 B2 U2 B2 L2 B2 R2
57. 2c + 2T
    R2 Us2 B' D2 Rs2 U2 F' R2 (10f*)
    L2 D2 R2 F2 (U2 B2 R2)² B2 R2 F2
58. 2H + 2c + 2T, type 1
    B2 R2 Ua' B2 L2 Ua F2 R2 U2 (11f*)
    B2 (R2 F2 U2)² B2 U2 F2 U2 R2 D2
59. 2D + 2T
    F2 R2 Ua' B2 R2 Ua F2 R2 U2 (11f*)
    (F2 R2 U2)² R2 F2 D2 (B2 L2)²
60. 2H + 2D + 2T, type 1
    Ra' U2 Fa' U2 Fa' Ra' U2 (11f*)
    (F2 R2 U2)² R2 F2 D2 B2 R2 F2 R2
61. 2H + 2c + 2T, type 2
    Fa' U2 Ra' D2 Ra' Fa' U2 (11f*)
    (L2 F2 U2)² F2 R2 U2 (L2 B2)²
62. 2X + 2c + 2T
    F2 L2 Ua' B2 R2 Ua B2 R2 U2 (11f*)
    (L2 F2 U2)² F2 R2 U2 R2 F2 R2 B2
63. 2H + 2D + 2T, type 2
    B2 L2 Ua' B2 L2 Ua B2 R2 U2 (11f*)
    (L2 F2 U2)² F2 L2 D2 R2 B2 L2 B2
64. 2X + 2D + 2T
    F2 U2 Ra B2 D2 L2 F2 U2 Ra' (11f*)
    (L2 F2 U2)² B2 R2 U2 (R2 B2)²
65. 2H + 4a
    R2 F Us2 F2 Us2 F' R2 (9f*)
    (F2 L2 U2)² R2 B2 U2 F2 L2 B2 L2
66. 2T + 2a
    L2 F' D2 Rs2 U2 B' R2 (8f*)
    (L2 F2 U2)² F2 R2 D2 R2 F2 L2 F2
67. 2H + 2T + 2a, type 1
    B2 L2 Ua' F2 L2 Ua' B2 R2 U2 (11f*)
    (L2 F2 U2)² B2 L2 U2 (R2 F2)²
68. 2H + 2T + 2a, type 2
    Fa' D' B2 Rs2 F2 U' Fa' (10f*)
    (L2 F2 U2)² F2 R2 D2 (R2 B2)²
69. 2X + 2T + 2a
    F2 R' U2 R2 Us2 R2 U2 R' F2 (10f*)
    (L2 F2 U2)² B2 L2 U2 R2 B2 L2 B2
70. 2H + 4c
    F2 R' F2 R2 Fs2 R2 F2 R' F2 (10f*)
    (F2 R2 U2)² R2 F2 U2 F2 R2 B2 R2
71. 2D + 2c
    F2 R' Ua Rs2 Ua' R' F2 (10f*)
    (R2 F2 U2)² B2 R2 U2 R2 F2 R2 B2
72. 2H + 2D + 2c, type 1
    L2 F2 B D2 Rs2 U2 F' R2 (9f*)
    (R2 F2 U2)² B2 R2 U2 (L2 B2)²
73. 2H + 2D + 2c, type 2
    R2 B2 Ua' R2 F2 Ua' R2 F2 U2 (11f*)
    (R2 F2 U2)² F2 L2 D2 (L2 F2)²
74. 2X + 2D + 2c
    Fs2 R2 B' D2 Rs2 U2 F' R2 (10f*)
    (R2 F2 U2)² F2 L2 D2 R2 B2 R2 F2
75. 2H + 4D
    L2 B2 F L2 Us2 R2 B' R2 (9f*)
    L2 (F2 U2)³ R2 U2 B2 L2 F2 U2

21. Symmetry m_er2_f, <(13)(24), (24)>, 4.

Suppose the r2 symmetry is centred on a face and that a plane of reflectional m_e symmetry contains this axis. Hold the cube so that the r2 symmetry is centred around the U/D faces.

The corners occur in four orbits, {URF, ULB} {DFR, DBL} {UFL, UBR} and finally {DLF, DRB}. The corners in any orbit can be swapped, but as this would be an odd permutation, another corner orbit would have to be swapped as well, or else some edges would need to move. All corners of an orbit lie in a plane of reflection, so they cannot be twisted and the corners cannot move out of its m_e plane. Therefore the only possible movements involving only corners are 9a-c (in either orientation).

The edges occur in four orbits. The FR and BL edges form one, the FL and BR edges the second, the U edges the third, and finally the D edges the fourth. The U edges can move in 3 ways; by 14b and by the following in either of its two orientations:

1. 2-swap of edges type 9 (UF,UL)(UB,UR)
   Fs2 U Rs2 D' Rs' Us2 Rs' (12f*)
   F2 R' B' R B F' R B' F' R B R' U' (14q*)

The U edges can be flipped as well, by 14c.

These same sequences can be used in different orientations to affect the D edges in the same manner. The U/D orbits can be swapped using 5f.

The middle layer edges can be moved by using 11b in a different orientation to swap the two orbits, 5f to swap the corners in each orbit, and 9f to flip one orbit. The only way to swap only the edges of one orbit is if the corners move as well, to make an even permutation, as follows:

2. Corner swap and edge swap type 2 (FR,BL)(URF,ULB)
   D2 L2 B D2 R2 F2 R2 B' D2 F2 L2 F' D2 F2 (14f*)

These patterns form a group of order 65,536 (= 2¹⁶). First I'll list those patterns involving 21a, which always mix adjacent colours on the sides.

3. (5f+21a)
   Fs2 U' F2 Rs2 F2 U Rs2 (10f*)
4. (21a+9f)
   D2 L B' U' L' B D2 F' R' D2 L2 D2 R2 U' F R' (16f*)
5. (5f+21a+9f)
   B2 L B L Fs2 D2 L D F D L' D R2 B L U F2 (18f*)
6. (9b'+21a)
   L2 B2 L2 D R2 B2 R2 F2 U L2 R2 U F2 U' (14f*)
7. (9b'+21a+9f)
   D B2 U R2 B2 U2 R' B' D2 U F2 D' B' D2 F R2 F R (18f*)
8. (9b'+5f+21a)
   L2 B2 U' L2 R2 U F2 R2 F2 L2 U' L2 U2 F2 U' (15f*)
9. (9b'+5f+21a+9f)
   D F2 U R2 F L' U' B2 F2 D R F L2 U' R2 U' (16f*)
10. (9c+21a)
    U B2 L2 D R2 U2 B2 L2 D2 B2 U F2 L2 D' (14f*)
11. (9c+21a+9f)
    U F2 L2 B L2 U L' D L U' Fs2 U R2 U B (16f*)
12. (9c+5f+21a)
    R2 D L2 U Fs2 U' F2 U' R2 D L2 D2 F2 D (15f*)
13. (9c+5f+21a+9f)
    Rs2 U R2 F2 L F2 L D R F L2 F' D R2 D' R' (17f*)
14. (9b'+9c+21a)
    D' B2 F2 D' B2 F2 D' F2 D2 U2 F2 U' (12f*)
15. (9b'+9c+21a+9f)
    B2 U F2 R2 D L2 F D L' D2 L D' F R2 D F2 D' (17f*)
16. (9b'+9c+5f+21a)
    B2 F2 D' B2 F2 D' U2 R2 D2 U2 R2 (11f*)
17. (9b'+9c+5f+21a+9f)
    B' F2 L' U L' B R B R B F U2 F' U' R2 (15f*)

All remaining patterns use opposing colours. First those patterns that involve 21b:

18. 4F (21b+9a')
    R2 D2 B2 U' B2 L2 U2 B2 L2 U B2 L2 D2 R2 U' (15f*)
19. (21b+14a)
    R2 B U2 F2 L2 F L2 U2 F2 R2 D2 F D2 F2 (14f*)
20. (21b+9a'+14a')
    L2 F U2 F2 L2 F L2 U2 F2 L2 U2 F U2 F2 (14f*)
21. (21b+5f)
    D2 R2 F' D2 L2 B2 R2 F' U2 F2 R2 F' U2 F2 (14f*)
22. 2X + 4F(21b+9a'+5f)
    R2 B L2 D2 F2 D2 B D2 R2 F2 R2 F D2 F2 (14f*)
23. (21b+14a+5f)
    F2 D2 F D2 R2 F2 R2 F D2 B2 L2 F R2 U2 (14f*)
24. (21b+9a'+14a'+5f)
    L2 B R2 D2 B2 D2 B' D2 R2 B2 R2 B' D2 F2 (14f*)
25. (21b+14b)
    L2 F U2 L2 F2 L2 F U2 F2 L2 F U2 F2 (13f*)
26. (21b+9a'+14b)
    F2 D2 L2 D F2 D2 F2 L2 U B2 L2 U2 F2 R2 U' (15f*)
27. (21b+14a+14b)
    R U' B2 D L' D' L2 U2 R D2 R F2 D2 R U (15f*)
28. Cube within a cube type 2 [p123] (21b+D2, 21b+9a'+14a'+14b)
    L2 F' L2 F2 U2 F' L2 F2 L2 U2 F' U2 F2 (13f*)
29. (21b+5f+14b)
    R2 F' L2 B2 D2 F' R2 F2 R2 D2 F' D2 F2 (13f*)
30. (21b+9a'+5f+14b)
    L2 U2 L2 B2 D' L2 F2 U2 L2 F2 D F2 U2 R2 U' (15f*)
31. (21b+14a+5f+14b)
    B2 L2 D2 L2 U' R2 B2 U2 F2 D F2 R2 U2 R2 U' (15f*)
32. (21b+9a'+14a'+5f+14b)
    R2 F U2 L2 B2 R2 F D2 F2 R2 F D2 F2 (13f*)
33. (21b+14b')
    B2 D2 R2 U F2 U2 B2 L2 D' B2 L2 U2 F2 R2 U' (15f*)
34. (21b+9a'+14b')
    L2 U2 F2 U F2 L2 D2 B2 R2 U' B2 R2 U2 R2 U' (15f*)
35. (21b+14a+14b')
    L2 U2 F2 U F2 L2 U2 B2 R2 D B2 R2 D2 R2 U' (15f*)
36. (21b+9a'+14a'+14b')
    B2 D2 F2 R2 D R2 D2 L2 F2 D F2 U2 F2 R2 U' (15f*)
37. (21b+5f+14b')
    F2 D2 F D2 R2 F2 R2 F D2 B2 L2 F R2 (13f*)
38. (21b+9a'+5f+14b')
    F2 R2 U2 L2 D R2 F2 D2 F2 U F2 R2 U2 R2 U' (15f*)
39. (21b+14a+5f+14b')
    F2 R2 U2 B2 L2 D' F2 R2 D2 R2 U F2 U2 R2 U' (15f*)
40. (21b+9a'+14a'+5f+14b')
    F2 D2 F' R2 F2 D2 F' R2 B2 L2 U2 F' R2 (13f*)
41. (21b+14b+14b')
    L2 B L2 D2 B2 U2 B U2 R2 B2 R2 F' U2 F2 (14f*)
42. (21b+9a'+14b+14b')
    R2 B' R2 U2 F2 D2 F' D2 L2 F2 L2 F' D2 F2 (14f*)
43. (21b+14a+14b+14b')
    L2 D2 F2 U' F2 R2 U2 B2 L2 D' B2 L2 U2 R2 U' (15f*)
44. (21b+9a'+14a'+14b+14b')
    U2 L2 F' D2 L2 F2 L2 F' D2 F2 L2 F' D2 F2 (14f*)
45. (21b+5f+14b+14b')
    R2 F' L2 U2 B2 D2 F D2 L2 B2 L2 F' D2 F2 (14f*)
46. (21b+9a'+5f+14b+14b')
    D2 R2 F U2 L2 B2 R2 F D2 F2 R2 F D2 F2 (14f*)
47. (21b+14a+5f+14b+14b')
    F2 R B2 L2 D2 R F2 R2 F2 D2 R D2 R2 U2 (14f*)
48. (21b+9a'+14a'+5f+14b+14b')
    R2 U2 R U2 F2 R2 F2 R U2 L2 B2 R F2 U2 (14f*)

The remaining patterns all use 14b, combined with a sequence from section 9 or 12 to restrict its symmetries.

49. (9a'+14b)
    D' L2 F' L2 D2 U2 R2 B' R2 D' (10f*)
50. (9a'+14b+5i)
    B2 D2 F2 L R B2 U2 F2 U2 L R (11f*)
51. (12a'+14b)
    D2 L2 F' L2 D2 U2 R2 B' R2 (9f*)
52. (12a'+14b+5i)
    F2 L2 D U B2 L2 D U B2 R2 (10f*)
53. (9a'+5f+14b)
    B2 U2 B2 L R B2 U2 F2 U2 L' R' (11f*)
54. (9a'+5f+14b+5i)
    F2 U2 F2 L R B2 D2 F2 U2 L' R' (11f*)
55. (12a'+5f+14b)
    F2 R2 D' U' B2 L2 B2 F2 D' U' F2 R2 (12f*)
56. (12a'+5f+14b+5i)
    U2 L2 B' U2 B2 F2 L2 R2 U2 F' R2 (11f*)

22. Symmetry m_fr2_f, <(13)(24), (12)(34)>, 4.

Suppose the r2 symmetry is centred on a face and that a plane of reflectional m_f symmetry contains this axis. Hold the cube so that the r2 symmetry is centred around the U/D faces. Note that this group of patterns includes those of sections 5, 10 and 11.

The corners occur in two orbits, the U corners and the D corners. The U corners can move in three ways, by 14a and by the following in either of its orientations:

1. 2-swap of corners, type 6 (URF,UFL)(UBL,URB)
   Fa R F' L F R' Fa' R B L' B' R' (14f*, 14q*)

They can be twisted:

2. 4-twist of corners, type 4 {URB+,ULF+,UBL-,UFR-}
   Fa D R2 F' Da B Da' F R2 D' Fa' U' (16f*)

These same sequences can be used in different orientations to affect the D corners in the same manner. The U/D orbits can be swapped using 5c.

The edges occur in 5 orbits. The middle layer's edges can move in three ways and be flipped, by using 5d, 5i and 11b in different orientations.

The other eight edges occur in pairs; {UL,UR} {UF,UB} {DL,DR} {DF,DB}. Each pair can be flipped, using the following sequence in some orientation.

3. 2-flip of edges, type 2 {UF+,UB+}
   U' F R' U F' Rs U B' R U' B Rs' (14f*,14q*)

Each pair can be swapped provided any other one is swapped as well to make it an even permutation. Any combination can be performed by using one of 10d, 11b, 14b in some orientation. Pairs can only be interchanged by using 11b because there is a plane of reflection through each vertical slice.

These patterns form a group of order 1,179,648 (= 2¹⁷3²).

There are rather many nice patterns in this group, but I will list them all anyway. First those which don't move any corners.

4. 2K, 2A
   D2 U' F2 U2 Fs2 U2 F2 U' (9f*)
5. 2H, 2K, 2A
   U L2 Fs2 R2 D' R2 Us2 R2 (10f*)
6. 2H, 2K, 2A
   F2 L2 U2 F2 Ra' U2 F2 Ra' (10f*)
7. 2X, 2K, 2A
   B2 L2 D2 F2 Ra U2 B2 Ra' (10f*)
8. 4A, 2H
   U B2 Rs2 F2 D' Rs2 (8f*)
9. 4K, 2H
   D' U2 L2 Fs2 R2 U' Rs2 (9f*)
10. 2K, 2A
    D2 L2 U2 L' B2 Us2 F2 R' U2 R2 (11f*)
11. 2K, 2A, 2X
    B2 L2 U2 F2 Ra U2 F2 Ra' (10f*)
12. 4A, 2H
    Rs2 D B2 Rs2 F2 U' (8f*,14q*)
13. 4K, 2H
    D' L2 Fs2 R2 U' Rs2 U2 (9f*)
14. 2K, 2A, 2H
    Rs2 U R2 Fs2 Us2 R2 D' (10f*)
15. 2K, 2A, 2H
    Fa R2 U2 Fa R2 U2 F2 R2 (10f*)

The following patterns move the corners by 5a, and therefore also use 10d to avoid the reflective symmetry through the middle layer.

16. 2U, 2t
    D R2 U2 Rs2 U2 R2 D' (8f*,14q*)
    L2 (U2 R2 F2)² R2 U2 F2 D2 R2
17. 2H, 2U, 2t
    B2 R2 U2 F2 Ra U2 F2 Ra' (10f*)
    (F2 U2)² F2 R2 F2 D2 R2 U2 F2 L2
18. 2U, 2t
    B2 L2 D2 B2 Ra' U2 F2 Ra' (10f*)
    (R2 D2)² R2 F2 L2 U2 B2 D2 R2 B2
19. 2H, 2U, 2t
    F2 R2 U2 B2 Ra D2 F2 Ra' (10f*)
    (F2 U2)² F2 R2 F2 D2 R2 D2 B2 R2
20. 2H, 2U, 2t
    Fs2 U L2 Fs2 Us2 L2 D' (10f*)
    (R2 F2 U2)² D2 R2 B2 R2 F2 U2 B2 R2
21. 2X, 2U, 2t
    R2 D2 R2 B2 Ua B2 R2 D2 L2 Ua' (12f*)
    (F2 U2)² B2 R2 F2 U2 L2 U2 F2 L2
22. 2H, 2U, 2t
    U L2 Fs2 Us2 L2 D' Fs2 (10f*)
    (R2 U2)² (R2 F2)² B2 D2 F2 U2 R2 F2
23. 2X, 2U, 2t
    L2 U2 L2 B2 Ua B2 R2 D2 L2 Ua' (12f*)
    (F2 U2)² B2 L2 B2 D2 R2 U2 F2 L2
24. 2H, 4t
    D' B2 Rs2 F2 U' Rs2 U2 (9f*)
    (R2 D2)² L2 F2 L2 U2 F2 D2 L2 F2
25. 2H, 4t
    D' U2 B2 Rs2 F2 U' Rs2 (9f*)
    (R2 U2)² L2 F2 L2 D2 B2 D2 R2 B2
26. 2H, 4U
    Rs2 D L2 Fs2 R2 U' (8f*,14q*)
    (F2 U2)² F2 L2 F2 U2 R2 D2 F2 R2
27. 2H, 4U
    U L2 Fs2 R2 D' Rs2 (8f*,14q*)
    (F2 U2)² F2 R2 F2 U2 R2 U2 B2 R2

These patterns move the corners by 5a', and again use 10d to avoid the reflective symmetry through the middle layer.

28. 2+, 2t, 2A
    B2 U2 Rs2 U2 F2 D B2 Rs2 F2 U' (12f*)
    (F2 R2 U2)² D2 B2 L2 F2 L2 U2 L2 B2
29. 2I, 2t, 2A
    U Rs2 U2 Rs2 U R2 Us2 R2 (11f*)
    (R2 U2)² L2 F2 R2 U2 B2 U2 R2 F2
30. 2+, 2t, 2A
    Ra D2 Fs2 Ra Fa U2 Fa (12f*)
    (F2 R2 U2)² D2 (B2 R2)² U2 L2 B2
31. 2I, 2t, 2A
    R2 Us2 R2 U' Fs2 U2 Fs2 U' (11f*)
    (R2 D2)² L2 B2 L2 U2 F2 D2 R2 F2
32. 2I, 2t, 2A
    Fa' L2 D2 Fa R2 U2 F2 R2 (10f*)
    (F2 D2)² B2 R2 F2 U2 R2 D2 B2 L2
33. 2O, 2t, 2A
    R2 F2 D2 L2 Fa' D2 L2 Fa' (10f*)
    (F2 D2)² F2 R2 F2 D2 L2 D2 B2 L2
34. 2I, 2t, 2A
    Fa' R2 D2 Fa R2 D2 F2 R2 (10f*)
    (F2 D2)² B2 R2 F2 U2 L2 U2 F2 R2
35. 2O, 2t, 2A
    D R2 F2 Us2 F2 R2 U' (8f*,14q*)
    (F2 D2)² F2 R2 F2 D2 R2 U2 F2 R2
36. 2+, 2t, 2K
    Rs2 D2 Fs2 D' B2 Rs2 F2 U' (11f*)
37. 2I, 2t, 2K
    Fs2 U' Fs2 U2 Fs2 U' (9f*)
38. 2+, 2t, 2K
    U2 Fs2 Rs2 D' B2 Rs2 F2 U' (11f*)
39. 2I, 2t, 2K
    U' Fs2 U2 Fs2 U' Fs2 (9f*)
40. 2I, 2t, 2K
    Rs2 D' Fs2 Ua' Rs2 U' (10f*)
41. 2O, 2t, 2K
    Fs2 D2 Fs2 D' L2 Fs2 R2 U' (11f*)
42. 2I, 2t, 2K
    D' Rs2 Ua' Fs2 U' Rs2 (10f*)
43. 2O, 2t, 2K
    U' L2 Fs2 R2 D' U2 (7f*,12q*)
44. 2+, 2U, 2A
    Fa R2 D2 Fa' L2 D2 F2 R2 (10f*)
45. 2I, 2U, 2A
    Fa U2 Fa Ra D2 Ra' (10f*,12q*)
46. 2+, 2U, 2A
    Fs2 Rs2 D L2 Fs2 R2 U' (10f*)
47. 2I, 2U, 2A
    F2 Rs2 F2 D L2 Fs2 R2 U' (10f*)
48. 2I, 2U, 2A
    Rs2 U' Rs2 D2 Rs2 U' (9f*)
49. 2O, 2U, 2A
    F2 R2 D2 F2 Ra' U2 F2 Ra' (10f*)
50. 2I, 2U, 2A
    U' Fs2 D2 Fs2 U' Rs2 (9f*)
51. 2O, 2U, 2A
    D B2 Rs2 F2 U' (6f*,10q*)
52. 2+, 2U, 2K
    B2 L2 D2 B2 Ra U2 F2 Ra' (10f*)
    (R2 U2)² L2 F2 R2 D2 F2 U2 R2 B2
53. 2I, 2U, 2K
    U2 D' F2 D2 Fs2 D2 F2 D' Rs2 (11f*)
    (F2 U2)² F2 R2 F2 D2 R2 U2 B2 R2
54. 2+, 2U, 2K
    F2 L2 D2 F2 R L D2 F2 R' L' (10f*)
    (F2 U2)² B2 R2 F2 U2 R2 D2 F2 L2
55. 2I, 2U, 2K
    Rs2 D2 U' F2 U2 Fs2 U2 F2 U' (11f*)
    (F2 U2)² F2 R2 F2 D2 L2 D2 F2 L2
56. 2I, 2U, 2K
    F2 R2 U2 B2 Ra' D2 F2 Ra' (10f*)
    (R2 D2)² R2 F2 L2 U2 F2 U2 L2 B2
57. 2O, 2U, 2K
    D R2 Fs2 L2 U' L2 D2 Rs2 D2 L2 (12f*)
    (R2 F2 U2)² D2 L2 F2 R2 F2 U2 F2 R2
58. 2I, 2U, 2K
    Fs2 U L2 D2 Rs2 D2 L2 U' (10f*)
    (R2 U2)² R2 F2 R2 U2 F2 D2 L2 F2
59. 2O, 2U, 2K
    D R2 Fs2 Us2 R2 U' (8f*,14q*)
    (R2 F2 U2)² D2 (R2 B2)² D2 B2 L2

These patterns move the corners by 14a, but do not use 10d.

60. 2T, 2a
    B2 Ua L2 B2 U2 L2 B2 Ua' R2 (11f*)
    (D2 F2 R2)² (B2 R2)² D2 R2 F2
61. 2H, 2T, 2a
    Rs2 D U2 F2 R2 Us2 R2 F2 U' (11f*)
    (D2 F2 R2)² (B2 L2)² D2 R2 B2
62. 2D, 2a
    D2 U R2 U2 Rs2 U2 R2 U' (9f*)
    (D2 F2 R2)² B2 L2 B2 R2 U2 L2 B2
63. 2H, 2D, 2a
    D2 Rs2 D F2 R2 Us2 R2 F2 U' (11f*)
    (D2 F2 R2)² B2 R2 F2 R2 D2 R2 B2
64. 2H, 2T, 2a [p128]
    Fs2 D U2 R2 Fs2 Us2 R2 U' (11f*)
    (D2 F2 R2)² (B2 R2)² D2 F2 B2 L2 B2 (antipode in square group)
65. 2X, 2T, 2a
    F2 Ua L2 F2 U2 L2 F2 Ua' R2 (11f*)
    (U2 R2 F2)² (L2 B2)² U2 B2 L2
66. 2H, 2D, 2a [p136]
    U2 Fs2 D F2 Rs2 Us2 F2 U' (11f*)
    (U2 R2 F2)² R2 F2 L2 F2 D2 Rs2 B2 L2 (antipode in square group)
67. 2X, 2D, 2a
    F2 Ua L2 B2 D2 R2 B2 Ua' R2 (11f*)
    (U2 R2 F2)² R2 F2 R2 B2 U2 B2 L2
68. 2T, 2c
    D' R2 U2 Rs2 U2 R2 D' (8f*,14q*)
    (U2 R2)³ B2 L2 U2 F2 D2 R2 F2
69. 2H, 2T, 2c
    U2 Rs2 D R2 F2 Us2 F2 R2 U' (11f*)
    (U2 F2)³ R2 F2 U2 L2 U2 B2 R2
70. 2D, 2c
    B2 U2 F' L2 Us2 R2 B' U2 F2 (10f*)
    (D2 R2)³ F2 R2 D2 F2 U2 L2 B2
71. 2H, 2D, 2c
    Rs2 D' R2 F2 Us2 F2 R2 U' (10f*)
    (U2 F2)³ R2 F2 U2 R2 D2 F2 L2
72. 2H, 2T, 2c [p129]
    D2 Fs2 D R2 Fs2 Us2 R2 U' (11f*)
    (U2 R2)³ F2 R2 Fs2 U2 F2 D2 R2 F2 (antipode in square group)
73. 2X, 2T, 2c
    F2 Ua R2 B2 D2 R2 F2 Ua' R2 (11f*)
    (U2 R2 F2)² L2 F2 R2 F2 U2 B2 L2
74. 2H, 2D, 2c [p131]
    Fs2 D' F2 Rs2 Us2 F2 U' (10f*)
    (U2 R2)³ F2 Us2 L2 U2 B2 U2 R2 B2 (antipode in square group)
75. 2X, 2D, 2c
    F2 Ua R2 F2 U2 L2 B2 Ua' R2 (11f*)
    (U2 L2 F2)² (L2 B2)² D2 F2 L2
76. 2H, 4a
    Rs2 D' B2 Rs2 F2 U' (8f*,14q*)
    (U2 F2 R2)² (F2 L2)² U2 R2 B2
77. 2c, 2a
    U Rs2 D2 Rs2 U' (7f*,12q*)
    (U2 F2 R2)² F2 L2 B2 L2 U2 R2 F2
78. 2H, 2c, 2a
    U2 Rs2 D B2 Rs2 F2 U' (9f*)
    (U2 F2 R2)² F2 R2 F2 L2 D2 L2 F2
79. 2H, 2c, 2a
    D L2 Fs2 R2 U' Fs2 U2 (9f*)
    (U2 R2 F2)² L2 F2 R2 F2 D2 B2 R2
80. 2X, 2c, 2a
    Fa D2 Fa Ra' D2 Ra' U2 (11f*)
    (D2 F2)² R2 U2 B2 L2 F2 U2 L2 U2 B2
81. 2H, 4c
    Rs2 U B2 Rs2 F2 D' U2 (9f*)
    (U2 F2 R2)² (B2 L2)² D2 L2 F2
82. 2H, 4T
    D' L2 Fs2 R2 U' Rs2 (8f*,14q*)
    (D2 R2 F2)² (R2 F2)² D2 B2 R2
83. 2D, 2T
    D' Ra Fs2 Ra' D' (8f*,10q*)
    (U2 R2)² B2 U2 L2 F2 R2 U2 B2 U2 L2
84. 2H, 2D, 2T
    D2 Rs2 U L2 Fs2 R2 D' (9f*)
    (D2 R2 F2)² L2 B2 L2 F2 D2 B2 R2
85. 2H, 2D, 2T
    D2 Fs2 D B2 Rs2 F2 U' (9f*)
    (U2 R2)³ F2 R2 D2 F2 D2 L2 F2
86. 2X, 2D, 2T
    Fs2 Rs2 U Fs2 U2 Fs2 U' (11f*)
    (D2 R2 F2)² L2 F2 R2 F2 U2 F2 R2
87. 2H, 4D
    Rs2 D U2 L2 Fs2 R2 U' (9f*)
    (D2 R2 F2)² L2 F2 R2 B2 D2 B2 R2

These patterns move the corners by 14a, and also use 10d.

88. 2V, 2 rectangle
    D2 R2 U2 Rs2 U2 R2 (7f*,14q*)
89. 2H, 2ct, 2 rectangle
    D2 Ra' Fs2 Ra' (7f*,10q*)
    Rs2 F2 L2 Us2 L2 F2 D2
90. 2ct, 2 rectangle
    D2 L2 Us2 R2 (5f*,10q*)
91. 2H, 2V, 2 rectangle
    Ra' Fs2 Ra' D2 (7f*,10q*)
    R2 D2 B2 R2 U2 R2 B2 L2
92. 2H, 2V, 2Y
    B2 Rs2 Us2 F2 U2 (7f*,14q*)
93. 2X, 2ct, 2Y
    B2 U2 Rs2 U2 F2 U2 (7f*,14q*)
94. 2H, 2ct, 2Y
    B2 Rs' Fs2 Rs' F2 U2 (9f*)
    Us Ra' Fs2 Ra' Ua' (12q*)
    D2 Fs2 R2 Fs2 Us2 R2
95. 2X, 2V, 2Y
    F2 Us2 F2 Rs2 U2 (7f*,14q*)
96. 2V, 2Y
    R2 B2 Rs2 Us2 F2 R2 U2 (9f*)
97. 2H, 2ct, 2Y
    U2 L2 F2 Us2 F2 R2 (7f*,14q*)
98. 2ct, 2Y
    B2 Ua' Rs2 Ua' F2 U2 (9f*,14q*)
    Fs2 R2 U2 Fs2 U2 R2 D2
99. 2H, 2V, 2Y
    L2 F2 Us2 F2 R2 U2 (7f*,14q*)
100. 2H, 2V, 2 rectangle
     U2 B2 Rs2 Us2 F2 (7f*,14q*)
101. 2X, 2ct, 2 rectangle
     U2 F2 Us2 F2 Rs2 (7f*,14q*)
102. 2H, 2ct, 2 rectangle
     D2 L2 Fs2 U2 Fs2 U2 R2 (9f*)
103. 2X, 2V, 2 rectangle
     U2 B2 U2 Rs2 U2 F2 (7f*,14q*)
104. 2H, 4 rectangle
     D2 Rs Fs2 Rs' (7f*,10q*)
     L2 B2 Rs2 F2 R2 U2 (7f*)
105. 2H, 2Y, 2 rectangle
     Rs Fs2 Rs' D2 (7f*,10q*)
     U2 L2 B2 Rs2 F2 R2 (7f*)
106. 2H, 4Y
     L2 Us' Rs2 Us' R2 U2 (9f*,14q*)
     Fs2 F2 (Rs2 B2)²
107. 2H, 4ct
     D2 Fs' Us2 Fs' (7f*,10q*)
     Fs2 U2 (R2 Fs2)²
108. 2H, 2V, 2ct
     Fs' Us2 Fs' D2 (7f*,10q*)
     (Fs2 R2)² U2 Fs2
109. 2H, 4V
     R2 Fs2 R2 D2 (5f*,10q*)
110. 2V, 2ct
     D2 Fa Us2 Fa' (7f*,10q*)
     Fs2 U2 F2 R2 Fs2 R2 F2
111. 2Y, 2 rectangle
     Rs2 D2 Rs2 (5f*,10q*)
112. 2X, 2V, 2ct
     Fs2 U2 Rs2 (5f*,10q*)
113. 2X, 2Y, 2 rectangle
     Rs2 Ua Rs2 Us (8f*,12q*)
     F2 R2 Fs2 R2 F2 D2 Rs2
114. 2H, 2V, 2ct
     D2 R2 Fs2 R2 (5f*,10q*)
115. 2H, 2Y, 2 rectangle
     L2 Fa' Us2 Fa' R2 U2 (9f*,14q*)
     Rs2 F2 Rs2 F2 D2 Fs2 (9f*)

These patterns move the corners by 10b, but do not use 10d.

116. 2+, 2T, 2a
     Fs2 D' L2 Fs2 R2 U' Rs2 (10f*)
     (U2 R2 F2)² (R2 B2)² U2 F2 R2
117. 2I, 2T, 2a
     U' L2 Fs2 R2 D' F2 Rs2 F2 (10f*)
     (D2 F2)² R2 D2 F2 R2 F2 U2 L2 U2 B2
118. 2+, 2D, 2a
     Rs2 D2 Fs2 D L2 Fs2 R2 U' (11f*)
     (F2 U2)² B2 U2 R2 F2 U2 R2 U2 B2 R2
119. 2I, 2D, 2a
     Fs2 D Fs2 Ua Rs2 U' (10f*)
     (D2 F2)² R2 U2 B2 R2 F2 U2 R2 U2 B2
120. 2I, 2T, 2a
     D2 Rs2 U' Fs2 U2 Fs2 U' (10f*)
     (U2 R2 F2)² (R2 F2)² U2 F2 L2
121. 2O, 2T, 2a
     U' B2 Rs2 F2 D' (6f*,10q*)
     (U2 F2 R2)² (F2 R2)² U2 L2 B2
122. 2I, 2D, 2a
     Rs2 U Fs2 U2 Fs2 U' (9f*)
     (U2 F2 R2)² F2 R2 F2 L2 D2 R2 B2
123. 2O, 2D, 2a
     Fs2 D2 Fs2 D B2 Rs2 F2 U' (11f*)
     (U2 F2 R2)² F2 L2 F2 R2 D2 R2 F2
124. 2+, 2T, 2c
     Fs2 D2 Rs2 D L2 Fs2 R2 U' (11f*)
     (U2 R2 F2)² R2 F2 L2 F2 U2 F2 R2
125. 2I, 2T, 2c
     Fs2 D Rs2 Ua Fs2 U' (11f*)
     (D2 R2)² F2 D2 R2 F2 L2 D2 B2 U2 R2
126. 2+, 2D, 2c
     Fs2 Rs2 D U2 L2 Fs2 R2 U' (10f*)
     (U2 R2 F2)² (L2 B2)² D2 B2 L2
127. 2I, 2D, 2c
     F2 Rs2 F2 D U2 L2 Fs2 R2 U' (11f*)
     (D2 R2)² F2 U2 R2 F2 L2 U2 B2 U2 R2
128. 2I, 2T, 2c
     Rs2 U Rs2 U2 Rs2 U' (9f*)
     (U2 F2 R2)² B2 R2 F2 R2 D2 R2 B2
129. 2O, 2T, 2c
     B2 Rs2 F2 U Rs2 U2 Rs2 U' (11f*)
     (U2 F2 R2)² B2 L2 F2 L2 D2 R2 F2
130. 2I, 2D, 2c
     D2 Rs2 U' Rs2 U2 Rs2 U' (10f*)
     (U2 F2 R2)² (B2 L2)² D2 R2 B2
131. 2O, 2D, 2c
     D U2 B2 Rs2 F2 U' (7f*,12q*)
     (U2 F2 R2)² (B2 R2)² D2 R2 F2
132. 2I, 4D
     R2 U2 R' B2 Us2 F2 L' U2 R2 (10f*)
     (U2 F2 R2)² (R2 F2)² D2 B2 R2
133. 2I, 4a
     U2 Fs2 U F2 U2 Fs2 U2 F2 U' (11f*)
     (U2 F2 R2)² (L2 B2)² U2 B2 R2
134. 2+, 2c, 2a [p132]
     L2 U2 Fs2 U2 R2 D' L2 Fs2 R2 U' (12f*)
     (U2 F2 R2)² R2 F2 R2 B2 U2 Rs2 F2 L2 (antipode in square group)
135. 2I, 2c, 2a
     U' F2 U2 Fs2 U2 F2 U' Fs2 (10f*)
     (U2 R2 F2)² R2 F2 R2 B2 U2 B2 R2
136. 2I, 2c, 2a
     R2 Us2 R2 U Fs2 D2 Fs2 U' (11f*)
     (D2 F2 R2)² B2 R2 B2 L2 U2 R2 B2
137. 2O, 2c, 2a
     D2 B2 R2 D2 F2 Ra' D2 F2 Ra' (11f*)
     (U2 R2 F2)² R2 B2 R2 F2 U2 B2 L2
138. 2I, 4c
     B2 Ua L2 B2 U2 R2 F2 Ua' R2 (11f*)
     (U2 R2 F2)² (R2 B2)² D2 F2 L2
139. 2I, 4T
     F2 Ua L2 B2 U2 L2 B2 Ua' R2 (11f*)
     (U2 F2 R2)² (B2 R2)² U2 R2 B2
140. 2+, 2D, 2T
     U2 B2 R2 U2 B2 Ra D2 F2 Ra' (11f*)
     (U2 F2 R2)² B2 R2 F2 R2 U2 R2 F2
141. 2I, 2D, 2T
     Fs2 D2 U R2 U2 Rs2 U2 R2 U' (11f*)
     (U2 F2 R2)² B2 L2 F2 L2 U2 R2 B2
142. 2I, 2D, 2T
     Rs2 U' F2 U2 Fs2 U2 F2 U' (10f*)
     (D2 R2 F2)² R2 B2 R2 F2 D2 F2 L2
143. 2O, 2D, 2T [p108]
     F2 U2 B U2 Rs2 D2 F' B2 D2 B2 (11f*)
     (R2 F2)² (D2 F2)² U2 L2 F2 (D2 R2)² (antipode in square group)

These patterns move the corners by 10b, and also use 10d.

144. 2+, 2V, 2Y
     Fs Us2 Fs' D2 (7f*,10q*)
     R2 Fs2 R2 U2 Fs2 (7f*)
145. 2I, 2ct, 2Y
     Us' Rs2 Ua' (6f*,8q*)
     R2 Us2 L2 F2 Us2 F2 U2
146. 2+, 2ct, 2Y
     U2 (Fs2 R2)² (7f*,14q*)
147. 2I, 2V, 2Y
     Fa Us2 Fa D2 (7f*,10q*)
     U2 F2 R2 Fs2 R2 F2
148. 2I, 2V, 2 rectangle
     Rs2 D2 (3f*,6q*)
149. 2O, 2ct, 2 rectangle
     D2 Rs' Fs2 Rs' (7f*,10q*)
     F2 Rs2 B2 Rs2 U2 Rs2
150. 2I, 2ct, 2 rectangle
     U2 Rs2 (3f*,6q*)
151. 2O, 2V, 2 rectangle
     U2 B2 Rs2 F2 (5f*,10q*)
152. 2+, 2V, 2 rectangle
     (Fs2 R2)² D2 (7f*,14q*)
153. 2I, 2ct, 2 rectangle
     Ua Rs2 Us' (6f*,8q*)
     D2 L2 Us2 R2 F2 Us2 F2
154. 2+, 2ct, 2 rectangle
     U2 Fs Us2 Fs' (7f*,10q*)
     Fs2 D2 R2 Fs2 R2 (7f*)
155. 2I, 2V, 2 rectangle
     U2 Fa' Us2 Fa' (7f*,10q*)
     F2 R2 Fs2 R2 F2 D2
156. 2I, 2V, 2Y
     Fs2 Rs2 U2 Fs2 (7f*)
     Us Fa Us2 Fa Ua (12q*)
157. 2O, 2ct, 2Y
     Us B2 Rs2 F2 Ua (8f*,12q*)
     R2 (Us2 F2)² L2 U2
158. 2I, 2ct, 2Y
     Fs2 D2 Fs2 Rs2 (7f*)
     Ua' Fa Us2 Fa Us (12q*)
159. 2O, 2V, 2Y
     Fs2 D2 F2 Rs2 F2 (7f*,14q*)
160. 2I, 2 rectangle, 2Y
     F2 Us2 F2 D2 (5f*,10q*)
161. 2+, 2 rectangle, 2Y
     D2 Fs2 L2 Fs2 Us2 R2 (9f*)
162. 2I, 4Y
     F2 Us2 F2 Rs2 U2 Rs2 (9f*)
163. 2I, 4 rectangle
     D2 R2 Us2 R2 (5f*,10q*)
164. 2O, 2Y, 2 rectangle
     F2 R2 Us2 R2 F2 U2 (7f*,14q*)
165. 2I, 2Y, 2 rectangle
     B2 L2 Fs2 Us2 R2 F2 U2 (9f*)
166. 2I, 2ct, 2V
     U2 R2 U2 Fs2 U2 R2 (7f*,14q*)
167. 2+, 2ct, 2V
     Fs2 D2 Ra' Fs2 Ra' (9f*,14q*)
     D2 Fs2 L2 F2 Us2 F2 R2
168. 2I, 4V
     Fs2 D2 R2 U2 Rs2 U2 R2 (9f*)
169. 2I, 4ct
     F2 U2 Rs2 U2 F2 U2 (7f*,14q*)
170. 2O, 2V, 2ct
     F2 Rs2 Us2 F2 U2 (7f*,14q*)
171. 2I, 2V, 2ct
     B2 R2 Fs2 R2 Us2 F2 U2 (9f*)

23. Symmetry r2_er2_e, <(13), (24)>, 4.

Hold the cube so that the r2 axes go through the middle layer. Note that this group of patterns includes those of sections 8, 9 and 10.

The corners lie in two orbits and, just as in section 9, they can move separately by 9a-c. This time however the corner orbits can be swapped, for example by 10a. The corners can only be twisted by 10c.

The U/D edges lie in two orbits, just as in section 10. Such an orbit can be flipped by 10e, and moved not only by 10d but by the following sequence and its mirror image:

1. 2-swap of edges (UR,DF)(UL,DB)
   U (Rm2 F2)² U' (8f*)
   U D2 Rs Fs2 Rs' U

These two orbits can also be swapped by 5g for example. The middle layer edges can only move exactly as in section 9.

These patterns form a group of order 98,304 (= 2¹⁵3).

There are surprisingly few new nice patterns in this group. There are two kinds; those with only opposite colours (which move the corners by 9a or 8b) and those with adjacent colours on the sides (which move the corners by 9c and/or 9b'). In either case the two orbits of the U/D layers must move differently so as to avoid extra symmetries we have seen before.

2. (9a+10d)
   R2 U2 L2 Fa R2 D2 L2 U2 Fa (11f*)
   (F2 L2)² (U2 F2)² R2 B2 R2 U2 F2
3. (9a+10d+5i)
   R2 U2 L2 Fa L2 U2 R2 U2 Fa (11f*)
   (F2 L2)² (U2 B2)² R2 F2 R2 U2 B2
4. (9a+5f+10d)
   L2 D2 L2 Fa R2 U2 L2 U2 Fa' (11f*)
5. (9a+5f+10d+5i)
   R2 D2 R2 Fa R2 D2 L2 U2 Fa' (11f*)
6. (8b+10d)
   R2 F2 Ua' R2 F2 Ua R2 F2 (10f*)
   F2 (R2 B2 D2)² F2 U2 B2 D2 L2
7. (8b+10d+5i)
   R2 F2 Ua L2 B2 Ua' R2 F2 (10f*)
   F2 (R2 B2 D2)² F2 D2 F2 U2 L2
8. (8b+5f+10d)
   Fa' Ra U2 Ra U2 Fa (10f*,12q*)
9. (8b+5f+10d+5i)
   Fa' Ra' D2 Ra' U2 Fa (10f*,12q*)

10. (23a+9f)
    D R2 F2 D U' L' D U' F' R2 B2 F' D U' R' U' (16f*)
    F U L R B2 R' F' U' F' R U' B L B' L R' U (18q*)
11. (9b'+23a)
    D U2 Ra Ua' Ra Ua Ra' U' (13f*,14q*)
12. (9b'+23a+9f)
    L' U' L' F' D L D2 U L U F D' F' D F2 U' (16f*,18q*)
13. (9c+23a)
    D' Ra' Ua Ra' Ua' Ra U' (12f*,12q*)
14. (9c+23a+9f)
    U' F2 L2 U2 R2 D2 R2 F Us' L U2 L' Us F U (17f*)
15. (9b'+9c+23a)
    D R2 Us2 R2 D U2 (7f*,12q*)
16. Python [p81] (9b'+9c+23a+9f)
    F2 R' B' U Rs' F' L Fs' D' R B L2 (14f*, 16q*)
17. (9d+23a)
    Fs2 Rs2 U' F2 Rs2 F2 U (10f*)
18. (9d+23a+9f)
    B2 U F2 D B2 L2 D' U F' L2 D F' R' B D B R (17f*)
19. (9b'+9d+23a)
    D' B2 U Rs2 U2 F2 Rs2 F2 U' F2 U'(13f*)
20. (9b'+9d+23a+9f)
    Rs2 U2 F2 D R2 U' L2 D R2 B2 F L D' L2 D L' F' U'
21. (9c+9d+23a)
    U B2 D F2 Us' L2 Fs2 U R2 U (12f*)
22. (9c+9d+23a+9f)
    B2 F U F U' F2 L2 F2 R' U2 B' U B2 L2 B' U R' (17f*)
23. (9b'+9c+9d+23a)
    U Fs2 U Fs2 R2 Us2 R2 U2 (11f*)
24. (9b'+9c+9d+23a+9f)
    L2 R B2 R2 F R2 U' B2 R F2 D2 L2 B2 F' R2 U' R2(17f*)

24. Symmetry r2_fr2_f, <(12)(34), (14)(23)>, 4.

Hold the cube so that the r2 axes go through the side face centres. Note that this group of patterns includes those of sections 8, 11 and 12.

The corners lie in two orbits just as in section 12, but they can move not only by 12a but also by using 12a in different orientations. The corner orbits can be swapped by for example 5b or 8a, and the only way they twist is by the supertwist 3a.

The edges in each slice form an orbit, and they can be moved in the usual way by using 11b and 5i in different orientations, and flipped by 5d.

These patterns form a group of order 294,912 (= 2¹⁵3²).

If the edge or corner orbits are swapped, then there will always be 3 colours on some faces. The only remaining essentially different ways for the corners to move that does not have m_f symmetry is by 12a or by 8b. With 12a, the m_e symmetry is only spoiled if the vertical slices move their edges differently. With 8b the r4 symmetry can be spoiled in the same way, and also by using 11b on the middle layer. This leads to 56 different patterns.

1. 2H + 4 deuce
   U2 F2 U2 B2 Ra F2 U2 F2 D2 Ra (12f*)
   (F2 R2)² (D2 F2)² L2 F2 R2 U2 B2 U2
2. 2 deuce + horizontal 2S
   Fa' Ra Fa Ra' Fa Ra (12f*, 12q*)
   (F2 R2)² (D2 F2)² L2 B2 L2 D2 F2 U2
3. 2H + 2 deuce + horizontal 2S, type 1
   U2 L2 U2 R2 Fa R2 D2 R2 U2 Fa (12f*)
   (F2 R2)² D2 B2 D2 (F2 L2)² U2 B2 D2
4. 2H + 2 deuce + horizontal 2S, type 2
   U2 B2 D2 F2 Ra F2 U2 F2 D2 Ra (12f*)
   (F2 R2)² (U2 F2)² R2 B2 L2 D2 B2 U2
5. 2X + 2 deuce + horizontal 2S
   R2 Ua' F2 Ua L2 Fa U2 Fa (12f*)
   (F2 R2)² (D2 B2)² R2 B2 L2 U2 B2 D2
6. 2H + horizontal 4S
   Ra U2 F2 D2 F2 Ra B2 D2 F2 U2 (12f*)
   (F2 R2)² (U2 F2)² L2 F2 R2 D2 B2 U2
7. 2H + vertical 2S + 2 deuce
   (U2 F2)² Ra (F2 U2)² Ra (12f*)
   (F2 R2)² (D2 B2)² L2 B2 R2 D2 B2 D2
8. Vertical 2S + Horizontal 2S
   Ra' U2 Ra B2 Ua R2 Ua F2 (12f*)
   (F2 R2)² (D2 B2)² L2 F2 L2 U2 F2 D2
9. 2H + vertical 2S + horizontal 2S, type 1
   U2 Ra F2 Ua R2 Ua' B2 Ra (12f*)
   (F2 R2)² (U2 F2)² L2 F2 L2 D2 F2 U2
10. 2H + vertical 2S + horizontal 2S, type 2
    Fa' Ra' Fa Ra Fa Ra (12f*, 12q*)
    (F2 R2)² (U2 B2)² R2 F2 L2 U2 B2 D2
11. 2X + vertical 2S + horizontal 2S
    D2 Fa R2 Ua F2 Ua R2 Fa (12f*)
    (F2 R2)² (D2 F2)² R2 F2 L2 D2 B2 U2
12. 2H + 2 diagonal + horizontal 2S
    Ra (U2 F2)² Ra F2 U2 F2 D2 (12f*)
    (F2 R2)² (U2 B2)² L2 B2 R2 U2 B2 D2
13. 2H + 2 deuce + vertical 2S, type 1
    Fa Ra Fa Ra' Fa' Ra (12f*, 12q*)
    (F2 R2)² (D2 F2)² L2 F2 R2 D2 F2 D2
14. 2 deuce + 2 diagonal
    B2 Ua R2 Ua F2 Ra' U2 Ra (12f*)
    (F2 R2)² (D2 F2)² L2 B2 L2 U2 B2 D2
15. 2H + 2 deuce + 2 diagonal, type 1
    Ra' Fa Ra Fa Ra' Fa (12f*,12q*)
    (F2 R2)² (D2 B2)² R2 F2 R2 U2 F2 D2
16. 2H + 2 deuce + 2 diagonal, type 2
    U2 Fa R2 Ua F2 Ua' L2 Fa (12f*)
    (F2 R2)² (U2 F2)² R2 B2 L2 U2 F2 D2
17. 2X + 2 deuce + 2 diagonal
    F2 Ua R2 Ua F2 Ra U2 Ra (12f*)
    (F2 R2)² (D2 B2)² R2 B2 L2 D2 F2 U2
18. 2H + horizontal 2S + 2 diagonal
    Ra Fa Ra' Fa Ra' Fa (12f*, 12q*)
    (F2 R2)² (U2 F2)² L2 F2 R2 U2 F2 D2
19. 2H + vertical 4S
    Ra' B2 Ua R2 Ua F2 Ra U2 (12f*)
    (F2 R2)² (D2 B2)² L2 B2 R2 U2 F2 U2
20. Vertical 2S + 2 diagonal
    Fa' U2 Fa R2 Ua F2 Ua' R2 (12f*)
    (F2 R2)² (D2 B2)² L2 F2 L2 D2 B2 U2
21. 2H + vertical 2S + 2 diagonal, type 1
    U2 Fa' L2 Ua F2 Ua R2 Fa (12f*)
    (F2 R2)² (U2 F2)² L2 F2 L2 U2 B2 D2
22. 2H + vertical 2S + 2 diagonal, type 2
    U2 Ra' B2 Ua R2 Ua F2 Ra (12f*)
    (F2 R2)² (U2 B2)² R2 F2 L2 D2 F2 U2
23. 2X + vertical 2S + 2 diagonal
    Ra' Fa Ra' Fa Ra Fa (12f*, 12q*)
    (F2 R2)² (D2 F2)² R2 F2 L2 U2 F2 D2
24. 2H + 4 diagonal
    U2 Ra F2 Ua R2 Ua B2 Ra' (12f*)
    (F2 R2)² (U2 B2)² L2 B2 R2 D2 F2 U2
25. Vertical 2S + 2 deuce
    D' R2 B2 D2 B2 R2 U2 L2 Us' R2 U' (12f*)
    D2 F2 U2 (L2 F2)² U2 F2 D2 (R2 F2)²
26. 2 diagonal + horizontal 2S
    D' R2 F2 D2 F2 R2 U2 L2 Us R2 U' (12f*)
    U2 (F2 L2)² D2 B2 D2 (F2 L2)² D2 B2
27. 2X + Vertical 2S + 2 deuce
    B2 L2 Ua (R2 F2)² Ua' F2 R2 (12f*)
    (F2 R2)² (U2 F2)² L2 B2 R2 U2 B2 U2
28. 2X + 2 diagonal + horizontal 2S
    B2 L2 Ua L2 F2 R2 B2 Ua' F2 R2 (12f*)
    (F2 R2)² (D2 F2)² L2 B2 R2 D2 B2 U2

29. 2+ + 2 deuce + vertical 2S
    U2 Ra B2 Ua R2 Ua F2 Ra (12f*)
    (F2 R2)² (U2 B2)² L2 B2 L2 U2 B2 U2
30. 2I + 2 deuce + vertical 2S
    Ra' Fa' Ra Fa Ra' Fa (12f*,12q*)
    (F2 R2)² (D2 B2)² R2 B2 L2 U2 F2 U2
31. 2+ + 2 deuce + 2 diagonal
    U2 Ra F2 Ua' R2 Ua' B2 Ra (12f*)
    (F2 R2)² (D2 B2)² R2 F2 R2 D2 B2 U2
32. 2I + 2 deuce + 2 diagonal, type 1
    R2 Ua' F2 Ua L2 Fa U2 Fa' (12f*)
    (F2 R2)² (U2 B2)² L2 F2 R2 D2 F2 U2
33. 2I + 2 deuce + vertical 2S
    F2 Ua R2 Ua' B2 Ra' D2 Ra (12f*)
    (F2 R2)² (D2 F2)² L2 B2 L2 D2 B2 D2
34. 2O + 2 deuce + vertical 2S
    (U2 R2)² Fa (L2 U2)² Fa (12f*)
    (F2 R2)² (U2 F2)² R2 B2 L2 D2 F2 D2
35. 2I + 2 deuce + 2 diagonal, type 2
    Fa Ra Fa Ra' Fa Ra (12f*,12q*)
    (F2 R2)² (U2 F2)² R2 F2 R2 U2 B2 D2
36. 2O + 2 deuce + 2 diagonal [p83]
    Fa (D2 R2)² Fa (R2 U2)² (12f*)
    (F2 R2)² (D2 F2)² L2 F2 R2 U2 F2 D2
37. 2+ + horizontal 2S + vertical 2S [p106]
    U2 Ra' F2 Ua R2 Ua B2 Ra' (12f*)
    (F2 R2)² (U2 B2)² R2 F2 R2 U2 B2 U2
38. 2I + horizontal 2S + vertical 2S, type 1
    Ra D2 Ra F2 Ua R2 Ua' F2 (12f*)
    (F2 R2)² (D2 B2)² L2 F2 R2 U2 F2 U2
39. 2+ + horizontal 2S + 2 diagonal
    Ra F2 Ua R2 Ua B2 Ra U2 (12f*)
    (F2 R2)² (D2 B2)² L2 B2 L2 D2 B2 U2
40. 2I + horizontal 2S + 2 diagonal, type 1
    Fa Ra Fa Ra Fa Ra' (12f*, 12q*)
    (F2 R2)² (U2 B2)² R2 B2 L2 D2 F2 U2
41. 2I + horizontal 2S + vertical 2S, type 2
    Ra Fa' Ra' Fa Ra' Fa (12f*, 12q*)
    (F2 R2)² (D2 F2)² R2 F2 R2 D2 B2 D2
42. 2O + horizontal 2S + vertical 2S
    D R2 F2 B D2 Rs2 U2 F' R2 U' (11f*)
    (F2 R2)² (U2 F2)² L2 F2 R2 D2 F2 D2
43. 2I + horizontal 2S + 2 diagonal, type 2
    Fa R2 Ua' B2 Ua R2 Fa U2 (12f*)
    (F2 R2)² (U2 F2)² L2 B2 L2 U2 B2 D2
44. 2O + horizontal 2S + 2 diagonal [p62]
    F2 R2 Ua L2 F2 L2 F2 Ua F2 R2 (12f*)
    (F2 R2)² (D2 F2)² R2 B2 L2 U2 F2 D2

45. 2I + 4 diagonal
    F2 L2 Ua' L2 B2 L2 B2 Ua F2 R2 (12f*)
    (F2 R2)² (D2 B2)² R2 B2 L2 D2 B2 D2
46. 2+ + 2 deuce + horizontal 2S
    Ra' Fa Ra Fa Ra' Fa' (12f*, 12q*)
    (F2 R2)² (D2 B2)² R2 F2 R2 U2 F2 D2
47. 2I + 2 deuce + horizontal 2S, type 1
    F2 Ua R2 Ua F2 Ra' U2 Ra (12f*)
    (F2 R2)² (U2 F2)² R2 F2 R2 D2 F2 U2
48. 2I + 2 deuce + horizontal 2S, type 2
    B2 Ua R2 Ua F2 Ra U2 Ra (12f*)
    (F2 R2)² (U2 B2)² L2 F2 R2 U2 B2 D2
49. 2O + 2 deuce + horizontal 2S
    D' Ra' Fa U2 Fa U2 Ra U' (12f*)
    (F2 R2)² (D2 F2)² L2 F2 R2 D2 B2 U2
50. 2I + horizontal 4S
    F2 L2 Ua' R2 B2 L2 F2 Ua F2 R2 (12f*)
    (F2 R2)² (U2 B2)² R2 B2 L2 U2 B2 D2
51. 2I + vertical 4S
    F2 L2 Ua R2 F2 R2 F2 Ua' F2 R2 (12f*)
    (F2 R2)² (D2 F2)² R2 F2 L2 D2 F2 U2
52. 2+ + vertical 2S + 2 diagonal
    F2 R2 Ua R2 F2 R2 B2 Ua' F2 R2 (12f*)
    (F2 R2)² (D2 F2)² R2 B2 R2 U2 B2 D2
53. 2I + vertical 2S + 2 diagonal, type 1
    B2 R2 Ua L2 F2 L2 B2 Ua' F2 R2 (12f*)
    (F2 R2)² (U2 B2)² R2 B2 R2 D2 B2 U2
54. 2I + vertical 2S + 2 diagonal, type 2
    F2 L2 Ua L2 B2 L2 F2 Ua' F2 R2 (12f*)
    (F2 R2)² (U2 F2)² L2 B2 R2 U2 F2 D2
55. 2O + vertical 2S + 2 diagonal
    Fa Ra' Fa Ra Fa Ra (12f*,12q*)
    (F2 R2)² (D2 B2)² L2 B2 R2 D2 F2 U2
56. 2I + 4 diagonal
    F2 L2 Ua L2 F2 R2 B2 Ua' F2 R2 (12f*)
    (F2 R2)² (U2 F2)² R2 F2 L2 U2 F2 D2