Snake Cubes / Cubra

Snake Cubes, also called chain cubes or elastic cubes, are puzzles consisting of 27 cubes connected together, usually by a piece of elastic. Every cube (except for the ones at either end) has two faces with a hole in their centre through which the elastic runs. A cube can have holes in opposite faces, so that the elastic runs straight through, or in adjacent faces, so that the elastic makes a 90 degree turn through the cube. The aim of the puzzle is to fold it into the shape of a 3×3×3 cube.

There are many versions of this puzzle. Some are made of wood, others of plastic, but more interesting is that different versions have different arrangements of 'straight' and 'bend' cubes on the string. Some of these arrangements are much easier than others. In general, those with more straights are easier because there are fewer degrees of freedom. On the other hand, some versions may have multiple solutions making it easier, too. The most difficult ones are those with unique solutions and not too many straights.

This puzzle should not be confused with the Kibble cube. That is also a string of cubes, but its cubes has slots that allow the elastic to change the faces it enters and exits. There are also versions of the snake cube where it is easy to make a cube, but where the aim is to make one with a particular colour pattern. I will not discuss those here.

One of the hardest versions of the snake cube is Kev's Kubes (version 9B), made by Trench Puzzles. It is made from wood, alternately coloured white and black. A plastic version called Cubra comes in 5 variations, each with a different colour. In order of difficulty, they are Mean Green, Bafflin' Blue, Twist yer 'ead Red, 'Orrible Orange, and Puzzlin' Purple. Almost all other versions of the snake cube have the same shape as the Cubra Blue.

If we denote the straights, corners, and ends with the letters S, C, and E, then the type of snake cube is easily given by a string of 27 letters. Here are the snake patterns some of the commercially available puzzles:

ESCCCSCSCCCCCCCCCCCCCSCSCCE	Kev's Kubes (9B)
ESCSCSCCSCSCSCCCCSCCSCCSCSE	Cubra Green
ESCSCSCSCCCCSCSCCCSCCSCCCSE	Cubra Blue
ESCCCCCCCCCSCCCCCCCSCSCCCCE	Cubra Red
ESCSCCCCSCCCCCCCCSCCCSCCCSE	Cubra Orange
ECCCCSCSCCCCCCCCCCCSCSCCCCE	Cubra Purple

The Cubra Red has 10 solutions, the Cubra Purple has 6, and all the rest have unique solutions (disregarding mirror images or rotations).

Analysis:

The string of cubes form a Hamiltonian path through a 3×3×3 grid graph. In other words, it is a path through the 27 points of a 3×3×3 grid, that visits each point exactly once.
I wrote a computer program that finds all such Hamiltonian paths, discarding any rotations or mirror images. The 51704 produced paths were then examined to see what string of straights and bends they form, which resulted in 11487 snakes. Of these, 3658 have unique solutions. The full results are listed in the tables below.

N u m b e r o f S o l u t i o n s	Number of Straights
		2	3	4	5	6	7	8	9	10	11	Total
	1	0	15	144	589	1053	1078	556	187	34	2	3658
	2	0	26	145	502	862	770	325	65	9	0	2704
	3	0	25	118	326	393	255	104	21	0	0	1242
	4	1	14	98	242	340	203	89	14	1	0	1002
	5	0	12	56	140	168	86	12	1	0	0	475
	6	1	11	57	123	181	97	23	3	0	0	496
	7	2	6	36	101	71	30	0	0	0	0	246
	8	0	8	35	89	83	43	22	7	1	0	288
	9	3	9	23	51	61	17	5	0	0	0	169
	10	0	10	33	57	34	16	6	0	0	0	156
	11	0	6	28	39	22	11	1	1	0	0	108
	12	2	4	30	39	35	17	9	1	0	0	137
	13	2	2	20	31	9	5	1	0	0	0	70
	14	0	6	23	25	24	10	0	0	0	0	88
	15	0	2	16	28	12	3	0	0	0	0	61
	16	0	3	15	24	11	7	5	3	1	0	69
	17	1	9	14	16	9	3	0	0	0	0	52
	18	1	3	9	6	10	7	1	0	0	0	37
	19	0	6	12	16	6	2	0	0	0	0	42
	20	0	1	11	18	11	1	0	0	0	0	42
	21	3	4	8	10	3	1	0	0	0	0	29
	22	1	6	10	7	2	1	0	0	0	0	27
	23	1	5	8	6	2	0	0	0	0	0	22
	24	0	2	8	7	6	3	0	0	0	0	26
	25	0	5	5	5	1	1	0	0	0	0	17
	26	1	0	8	5	3	1	0	0	0	0	18
	27	1	2	6	5	4	0	0	0	0	0	18
	28	1	1	10	2	1	1	0	0	0	0	16
	29	0	1	4	5	0	0	0	0	0	0	10
	30	0	0	4	3	1	4	0	0	0	0	12
	31	0	3	1	7	1	0	0	0	0	0	12
	32	0	2	4	6	2	0	0	0	0	0	14
	33	0	1	3	3	3	1	0	0	0	0	11
	34	0	2	3	0	4	0	0	0	0	0	9
	35	0	1	1	2	0	0	0	0	0	0	4
	36	0	0	0	2	0	0	0	0	0	0	2
	37	0	2	1	1	0	0	0	0	0	0	4
	38	0	1	1	1	0	0	0	0	0	0	3
	39	0	0	4	2	0	0	0	0	0	0	6
	40	0	0	0	1	3	0	0	0	0	0	4
	41	0	0	1	0	1	0	0	0	0	0	2
	42	0	0	1	0	3	0	0	0	0	0	4
	43	1	2	0	0	1	0	0	0	0	0	4
	44	0	1	0	3	1	0	0	0	0	0	5
	45	0	0	0	2	1	0	0	0	0	0	3
	46	0	1	1	0	0	0	0	0	0	0	2
	47	0	1	1	2	2	0	0	0	0	0	6
	48	0	2	0	0	1	0	0	0	0	0	3
	49	0	0	0	1	0	0	0	0	0	0	1
	50	0	1	1	1	0	0	0	0	0	0	3
	51	0	0	1	1	0	0	0	0	0	0	2
	52	0	0	1	0	1	0	0	0	0	0	2
	53	0	0	1	1	0	0	0	0	0	0	2
	54	0	2	0	0	0	0	0	0	0	0	2
	55	0	2	0	0	0	0	0	0	0	0	2
	56	1	0	1	0	0	0	0	0	0	0	2
	57	0	0	2	0	1	0	0	0	0	0	3
	58	0	0	1	0	0	0	0	0	0	0	1
	61	0	1	1	0	0	0	0	0	0	0	2
	62	1	1	0	3	0	0	0	0	0	0	5
	64	0	0	1	0	0	0	0	0	0	0	1
	67	0	0	0	1	0	0	0	0	0	0	1
70	0	1	0	1	1	0	0	0	0	0	3
71	0	1	0	0	0	0	0	0	0	0	1
73	0	0	1	0	0	0	0	0	0	0	1
81	0	0	1	0	0	0	0	0	0	0	1
85	0	0	0	1	0	0	0	0	0	0	1
86	0	0	1	0	0	0	0	0	0	0	1
87	0	0	1	0	0	0	0	0	0	0	1
88	0	0	2	2	0	0	0	0	0	0	4
90	0	0	1	1	0	0	0	0	0	0	2
104	0	1	1	0	0	0	0	0	0	0	2
112	0	1	0	0	0	0	0	0	0	0	1
115	0	0	0	1	0	0	0	0	0	0	1
119	0	0	1	0	0	0	0	0	0	0	1
123	0	1	0	0	0	0	0	0	0	0	1
126	0	0	1	0	0	0	0	0	0	0	1
142	0	0	1	0	0	0	0	0	0	0	1
Total	24	235	1037	2563	3444	2674	1159	303	46	2	11487

The following is a similar table, but counting only those snake patterns that are palindromic, i.e. sequences of straights and bends which look the same when reversed, such as the Cubra Purple.

	2	3	4	5	6	7	8	9	10	Total
1	0	0	5	4	6	10	2	1	1	29
2	0	0	1	1	3	3	1	0	0	9
3	0	0	0	3	1	0	1	2	0	7
4	1	1	2	2	1	2	0	0	0	9
5	0	0	0	0	2	2	0	0	0	4
6	0	0	1	0	1	0	0	0	0	2
7	0	0	0	3	0	0	0	0	0	3
9	0	1	0	0	0	1	0	0	0	2
10	0	1	0	0	0	0	0	0	0	1
11	0	0	1	0	0	0	0	1	0	2
13	1	0	0	1	0	0	0	0	0	2
17	0	0	1	0	0	0	0	0	0	1
19	0	0	0	1	0	0	0	0	0	1
21	1	0	0	0	0	0	0	0	0	1
22	0	1	0	0	0	0	0	0	0	1
25	0	0	1	0	0	0	0	0	0	1
31	0	1	0	0	0	0	0	0	0	1
45	0	0	0	1	0	0	0	0	0	1
Total	3	5	12	16	14	18	4	4	1	77

As you can see, it is impossible to form a cube using a snake with only bends in it. It is possible to use longer snakes without straights to form a 5×5×5 cube, or a 3×5×7 block. Blocks with one or more even dimensions, such as a 2×2×2 cube, tend to be too easy.

I'll just list some of the outliers in the above tables.

The two snakes with 11 straights:
ESCSCSCCSCSCSCCSCSCSCCSCCSE
ESCCSCCSCSCSCSCSCSCSCCSCSCE
The 15 snakes with 3 straights and unique solutions:
ECCCCCCCCSCSCCCSCCCCCCCCCCE     ECCCCCCCSCCSCSCCCCCCCCCCCCE
ECCCCCCSCCCSCSCCCCCCCCCCCCE     ECCCCSCCCCCCCCCSCCSCCCCCCCE
ECCCCSCCCCCCCSCCCSCCCCCCCCE     ECCCCSCCCCCSCCCSCCCCCCCCCCE
ECCCCSCCCSCCCCCCCSCCCCCCCCE     ECCCCSCCCSCCCSCCCCCCCCCCCCE
ECCCCSCCSCCCCCCCCSCCCCCCCCE     ECCSCCCSCCCCCSCCCCCCCCCCCCE
ECSCCSCCCCCCCCCCCCCSCCCCCCE     ESCCCCCCCCSCCCCCCCCCCCCCCSE
ESCCCCCCCSCCCSCCCCCCCCCCCCE     ESCCCSCCCCCCCCCCCCCCCSCCCCE
ESCCCSCCCCCCCSCCCCCCCCCCCCE
The palindromic snakes with unique solutions (followed by the number of straights):
ECCCCSCCCCCSCCCSCCCCCSCCCCE   4
ESCCCCCCCCCSCCCSCCCCCCCCCSE   4
ESCCCCCCCSCCCCCCCSCCCCCCCSE   4
ESCCSCCCCCCCCCCCCCCCCCSCCSE   4
ECCCCSCCSCCCCCCCCCSCCSCCCCE   4
ECCCCCCCSCCSCSCSCCSCCCCCCCE   5
ESCCSCCCCCCCCSCCCCCCCCSCCSE   5
ECCCCSCSCCCCCSCCCCCSCSCCCCE   5
ECCCCCSCCSCCCSCCCSCCSCCCCCE   5
ECCSCSCCSCCCCCCCCCSCCSCSCCE   6
ESCCSCCCCCCSCCCSCCCCCCSCCSE   6
ESCCSCCCSCCCCCCCCCSCCCSCCSE   6
ECCCCSCSCCSCCCCCSCCSCSCCCCE   6
ECCSCSCSCCCCCCCCCCCSCSCSCCE   6
ECCSCSCCCCCSCCCSCCCCCSCSCCE   6
ESCCCCCCSCCSCSCSCCSCCCCCCSE   7
ECCSCCCCCSCSCSCSCSCCCCCSCCE   7
ESCSCCCCSCCCCSCCCCSCCCCSCSE   7
ESCCCCSCCSCCCSCCCSCCSCCCCSE   7
ECSCCSCSCCCCCSCCCCCSCSCCSCE   7
ECSCCCCSCSCCCSCCCSCSCCCCSCE   7
ECCCCSCSCSCCCSCCCSCSCSCCCCE   7
ESCCSCCCCCCSCSCSCCCCCCSCCSE   7
ECSCCCCCCSCSCSCSCSCCCCCCSCE   7
ECCSCSCSCCCCCSCCCCCSCSCSCCE   7
ESCSCSCCCCSCCCCCSCCCCSCSCSE   8
ESCCSCSCCSCCCCCCCSCCSCSCCSE   8
ESCSCSCCSCCCCSCCCCSCCSCSCSE   9
ESCCSCCSCSCCSCSCCSCSCCSCCSE   10
Some of the snakes with most solutions:
ESCCSCCSCSCCCCCCCCCCCCCCCCE   90
ECCCCCCSCSCCSCCSCSCCCCCCCCE   90
ESCSCCCCCSCCCCCCCCCCCCCCCCE   104
ECCSCSCSCSCCCCCCCCCCCCCCCCE   104
ECCCCSCSCSCCCCCCCCCCCCCCCCE   112
ESCSCSCSCSCCCCCCCCCCCCCCCCE   115
ESCSCSCSCCCCCCCCCCCCCCCCCCE   119
ESCSCSCCCCCCCCCCCCCCCCCCCCE   123
ECCCCSCSCSCSCCCCCCCCCCCCCCE   126
ECCCCCCSCSCSCSCCCCCCCCCCCCE   142
Some of the palindromic snakes with most solutions:
ESCCCCCCCCCCCCCCCCCCCCCCCSE   21
ESCCCCCCCCCCCSCCCCCCCCCCCSE   22
ECCCCCCSCSCCCCCCCSCSCCCCCCE   25
ECCCCCCCCCCSCSCSCCCCCCCCCCE   31
ECCCCCCCCSCSCSCSCSCCCCCCCCE   45

General hints:

If the cubes of the snake alternate in colour, it is clear that one colour, e.g. white, has one more cube than the other. The finished cube will also have cubes alternating in colour, and it follows that the white cubes form the corners and face centres.
The two ends of the cube must therefore also be at corners and/or centres.

If the snake has several straights close to each other, try to solve that section first.

If the snake has a straight that is white (same colour as the snake's ends) then it must lie at a face centre. It is often useful to start solving from there.

Solutions:

The solutions will also be given using the letters F, L, U, B, R, D standing for the six directions in space where the next cube might be, viz. Front, Left, Up, Back, Right, Down respectively.

Kev's Kubes (9B):

As mentioned before, this is one of the hardest snake cubes. One contributing factor is that the ends of the snake both lie in face centres, not at corners.

RR F D LL BB R U L U R F L F D R U R BB DD F L

Cubra Green:

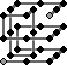RR BB LL U RR FF LL U R B DD L UU B RR FF

Cubra Blue:

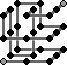RR BB LL UU R D R FF LL U B DD R UU F R BB

Cubra Red:

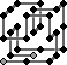	RR B U F U L D L U BB R D F U R B DD LL U F D R
	RR B U F U L D L U BB D F R D L B RR UU F L B D
	RR B U F U L D L U BB D R U F R B DD LL F U R D
	RR B U F U L D L U BB D R U F R B DD LL F R U L
	RR B U F U B L F D BB L D F R B R UU LL F D F U
	RR B U F U B L B R DD L U F D L B UU FF R D L B
	RR B U F L U R B L DD L B U R D R UU LL F D F U
	RR B U F L B U L B DD R F L U F U RR BB L D R D
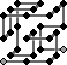	RR B U F L B D L B UU R F L D F U RR BB D L D R
	RR B L B R U L U R FF D B L U F L BB DD F U F R

Cubra Orange:

RR BB L U R FF L U L D B U B DD F R UU B R FF

Cubra Purple:

	R B L B UU RR F L D L U F D R U R DD BB L U R F
	R B L B UU RR F L D B D R U F D F UU LL B D F R
	R B L B RR UU F L B L D R F R D F UU LL B D F R
	R B L B RR UU F L B D L U F D F U RR DD B U L F
	R B R F UU LL B R D B D R U F U B LL DD F U F R
	R B R F UU LL B R B L D R F R U B DD LL F U F R

Jaap's Puzzle Page

Snake Cubes

Javascript Snake Cube

Links to other useful pages:

Analysis:

General hints:

Solutions: