Slide Rule Duel Pentaplenty and Heptalive

These Slide Rule Duel puzzles have pieces which in the top half of the frame form two large circle segments, and in the bottom half only one small circle segment. The bottom half can slide left and right so that its segment can line up with either of the top parts to make a complete disc, which can then be rotated.

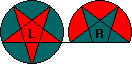Pentaplenty solved position The Pentaplenty has, as the name suggests, discs with 5-fold symmetry. Each disc has a pentagonal centre, five pointy pieces around that which form a pentagram, and five outer pieces between those points that fill up the rest of the disc. In the solved position, the left disc is complete and shows a red pentagram in a blue disc, and the right (partial) circle has reverse colours, i.e. a blue pentagram in a red disc.

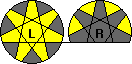Heptalive solved position The Heptalive on the other hand has 7-fold symmetry. Each circle has a heptagonal centre, seven tiny triangular pieces round it, seven pointy pieces around that which form a heptagram, and seven outer pieces between those points that fill up the rest of the circle. The sliding circle segment contains one tiny triangle, two pointy pieces, and three outer pieces. In the solved position, the left circle is complete and shows a yellow heptagram in a black circle, and the right (partial) circle has reverse colours, i.e. a black heptagram in a yellow circle.

These puzzles were invented by Douglas A. Engel, who also invented various other puzzles such as:

	Tiny triangles	Points	Outer pieces	Number of positions
Pentaplenty	-	5+4	5+3	9!·8! / 5!²·4!·3! =	7,056
Heptalive	7+6	7+5	7+4	13!·12!·11! / 7!³·6!·5!·4! =	448,493,760

I have used a computer to calculate God's algorithm for the Pentaplenty, and the results in the table below show that any position can be solved in at most 10 moves (6.9182 on average), or 14 (9.3849 on average) if every 1/5 of a turn is counted as a separate move.

	Total	1	4	16	54	176	554	1461	2424	1901	449	16	7056
		Face turn metric
S i n g l e t u r n m e t r i c		0	1	2	3	4	5	6	7	8	9	10	Total
	0	1											1
	1		2										2
	2		2	4									6
	3			8	8								16
	4			4	24	14							42
	5				22	50	24						96
	6					70	114	36					220
	7					42	207	202	38				489
	8						163	498	276	21			958
	9						46	509	826	186	4		1571
	10							198	930	686	37		1851
	11							18	326	767	156	3	1270
	12								28	237	192	4	461
	13									4	58	8	70
	14										2	1	3

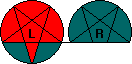
The single position that is antipodal in both metrics is shown on the right. Apart from the sliding bottom half, each circle is a single colour. Using the move notation below, it is reached by the move sequence R' L' R R L R R L' R R L R' L L.

The results for the Heptalive in the table below show that any position can be solved in at most 16 moves (12.119 on average), or 26 (20.147 on average) if every 1/7 of a turn is counted as a separate move.

	Total	1	6	36	202	1,100	6,250	34,952	191,708	1,017,927	5,104,217	22,757,253	79,777,382	170,354,129	140,483,580	27,600,973	1,153,936	10,108	448,493,760
		Face turn metric
S i n g l e t u r n m e t r i c		0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	Total
	0	1																	1
	1		2																2
	2		2	4															6
	3		2	8	8														18
	4			12	24	14													50
	5			8	48	58	28												142
	6			4	56	144	142	48											394
	7				48	234	427	318	74										1,101
	8				18	276	875	1,154	628	110									3,061
	9					226	1,305	2,806	2,818	1,174	138								8,467
	10					114	1,420	5,138	8,262	6,261	1,805	156							23,156
	11					34	1,124	6,989	17,927	22,047	11,997	2,522	150						62,790
	12						645	7,424	29,576	56,255	51,476	20,050	2,938	114					168,478
	13						232	5,845	38,386	110,544	158,549	103,625	27,142	2,502	58				446,883
	14						52	3,407	38,604	171,526	373,227	385,146	167,283	26,377	1,122	14			1,166,758
	15							1,427	29,877	209,519	691,047	1,094,207	751,507	186,942	13,263	202			2,977,991
	16							346	17,112	199,622	1,004,979	2,436,734	2,595,314	985,787	104,209	1,954	4		7,346,061
	17							50	6,692	142,685	1,131,625	4,226,136	7,013,573	4,066,135	618,419	15,065	42		17,220,422
	18								1,572	71,496	937,118	5,525,037	14,504,573	13,169,684	2,901,964	94,925	368		37,206,737
	19								164	22,678	531,064	5,078,362	21,564,104	32,011,047	10,742,519	489,951	2,716		70,442,605
	20								16	3,794	180,143	2,915,588	20,509,708	52,344,602	29,091,028	2,024,841	15,298	4	107,085,022
	21									214	29,455	867,726	10,372,801	47,425,484	48,583,904	6,074,783	69,676	46	113,424,089
	22									2	1,586	99,244	2,145,731	18,084,505	38,096,170	10,451,350	241,072	346	69,120,006
	23										8	2,712	121,630	2,013,026	9,808,165	7,170,687	470,704	1,826	19,588,758
	24											8	926	37,884	519,953	1,248,467	315,300	4,689	2,127,227
	25												2	40	2,806	28,722	38,379	3,051	73,000
	26															12	377	146	535

Notation:

A clockwise turn of the left or right disc of one step will be denoted by the letters L or R respectively. Turning a disc anti-clockwise one step will be denoted by L' or R'.

Solution:

Hold the puzzle with the slider at the bottom.

Phase 1: Solve the points and outer pieces of the right disc.

Make sure at least one point piece matching the right centre colour lies in the right disc. Rotate the right disc to bring this solved point piece to the bottom right, adjacent to the slider.
Find a point piece in the left disc that has the same colour as the right centre. If there are none in the left disc, then do R' L R and look again.
Rotate the left disc until that point piece lies in the bottom section, or bottom-right in the Heptalive. Then do R' to put it in place in the right disc.
If the outer piece adjacent to the point piece you just solved is already of the correct colour (different to the point piece) then skip to step g.
Find an outer piece in the left disc that has the same colour as the left centre. Turn the left disc so that that outer piece lies at the right of the bottom section.
The next step is slightly different for the two puzzles:
Pentaplenty: L' (R L' R' L) (L R L' R' )
Heptalive: L' (R L' R' L) (L L R L' L' R' )
Repeat steps b-f until all the points and outer pieces are solved.

It is fairly easy to solve phase 1 in far fewer moves by solving the pieces in pairs rather than individually by the steps above. Whenever there are two adjacent pieces (point and outer piece) in the left disc that belong on the right, you can solve them at the same time by adding them to either end of block of solved pieces on the right disc. If there is no such adjacent pair, it takes a little ingenuity to bring them together in the left disc, and then you can solve them as a pair as before.

Phase 2: Solve the tiny triangle pieces. (Heptalive only)

Rotate the left disc to bring any incorrect tiny piece to the bottom and do L' so it points bottom right.
Rotate the right disc to bring one of its incorrect pieces to the bottom.
Do (L R L' R' ) (L R L' R' )
Rotate the right disc back to its normal position, undoing the move from step b.
Repeat step a-d until all the tiny pieces are solved.

Jaap's Puzzle Page

Slide Rule Duel: Pentaplenty and Heptalive

The number of positions:

Links to other useful pages:

Notation:

Solution: