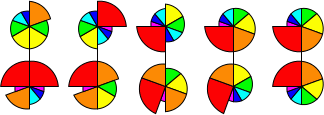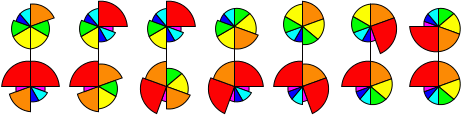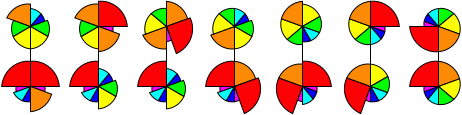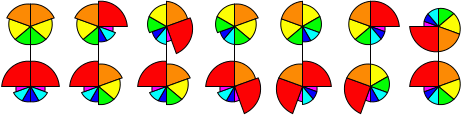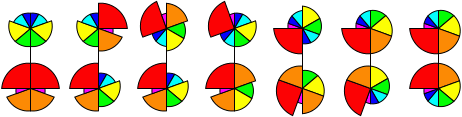Nautilus
Nautilus is a colourful puzzle in the shape of a Nautilus shell. It is mechanically similar
to the Square-1, as it has three layers, where the middle layer is
split through the middle into two halves. When solved, the top and bottom layers each consist of
seven pieces arranged like slices around the centre point. The seven pieces in a layer have
different angular sizes, namely 20, 30, 40, 50, 60, 70, and 90 degrees, and are coloured like
a rainbow from violet to red. The outer layers can rotate about their centre point. If both layers
are rotated such that the seam through the middle layer lines up with seams between the pieces, then
you can turn over half the puzzle, mixing the pieces from the two outer layers together.
The puzzle was designed by Tim Selkirk, and produced by Uwe Meffert.
The number of positions:
As this puzzle is so heavily bandaged, it is not possible to calculate the number
of positions, and you have to simply enumerate them all by trying all possible move
sequences (i.e. find God's algorithm). It turns out that the movements are so restricted
that it is impossible to swap two pieces of the same size, and even that the arrangement
of pieces in one outer layer determines the order of the pieces in the other.
I consider one half of the middle layer as fixed in space. The other half of the
middle layer has two possible positions. If positions that differ by turns of the top
or bottom layers are considered the same, then there are 326 possible arrangements of
the outer layers, giving 652 positions. If we count twistable arrangements, those in
which it is possible to twist the middle layer, then there are 2016 arrangements of the
pieces, or 4032 positions all together. Note that this shows that on average a layer has
sqrt(2016/326) = 2.48 orientations in which it lines up with the seam, i.e. there are on
average 1.24 cuts per layer.
I have used a computer to calculate God's algorithm for the puzzle. The results in the table below show that
the pieces can be solved in at most 12 twists (4.9939 on average), or 13 if you want to solve the middle
layer as well (5.4969 on average). If you count all outer layer turns as moves too, then it takes 27 moves
(12.608 on average), or 28 with the middle layer (13.298 on average).
| Excluding the middle layer |
|---|
| Turn metric: |
Turn metric
Twistable positions: |
Twist metric: |
| 0 | 1 |
|---|
| 1 | 71 |
|---|
| 2 | 1301 |
|---|
| 3 | 1654 |
|---|
| 4 | 8001 |
|---|
| 5 | 12543 |
|---|
| 6 | 25673 |
|---|
| 7 | 37216 |
|---|
| 8 | 18908 |
|---|
| 9 | 41696 |
|---|
| 10 | 37232 |
|---|
| 11 | 31104 |
|---|
| 12 | 39220 |
|---|
| 13 | 7700 |
|---|
|
| 14 | 28240 |
|---|
| 15 | 34584 |
|---|
| 16 | 14984 |
|---|
| 17 | 5736 |
|---|
| 18 | 9808 |
|---|
| 19 | 5192 |
|---|
| 20 | 9800 |
|---|
| 21 | 560 |
|---|
| 22 | 5192 |
|---|
| 23 | 5760 |
|---|
| 24 | 19600 |
|---|
| 25 | 1120 |
|---|
| 26 | 10352 |
|---|
| 27 | 9248 |
|---|
| Total | 422496
= 326*36*36 |
|---|
|
| 0 | 1 |
|---|
| 1 | 7 |
|---|
| 2 | 17 |
|---|
| 3 | 42 |
|---|
| 4 | 97 |
|---|
| 5 | 147 |
|---|
| 6 | 193 |
|---|
| 7 | 188 |
|---|
| 8 | 180 |
|---|
| 9 | 144 |
|---|
| 10 | 128 |
|---|
| 11 | 144 |
|---|
| 12 | 100 |
|---|
| 13 | 116 |
|---|
|
| 14 | 104 |
|---|
| 15 | 56 |
|---|
| 16 | 32 |
|---|
| 17 | 32 |
|---|
| 18 | 24 |
|---|
| 19 | 32 |
|---|
| 20 | 16 |
|---|
| 21 | 32 |
|---|
| 22 | 40 |
|---|
| 23 | 64 |
|---|
| 24 | 32 |
|---|
| 25 | 32 |
|---|
| 26 | 16 |
|---|
| Total | 2016 |
|---|
|
| 0 | 1 |
|---|
| 1 | 16 |
|---|
| 2 | 49 |
|---|
| 3 | 66 |
|---|
| 4 | 40 |
|---|
| 5 | 36 |
|---|
| 6 | 42 |
|---|
| 7 | 20 |
|---|
| 8 | 8 |
|---|
| 9 | 8 |
|---|
| 10 | 8 |
|---|
| 11 | 16 |
|---|
| 12 | 16 |
|---|
| Total | 326 |
|---|
|
| Including the middle layer |
|---|
| Turn metric: |
Turn metric
Twistable positions: |
Twist metric: |
| 0 | 1 |
|---|
| 1 | 71 |
|---|
| 2 | 1301 |
|---|
| 3 | 1656 |
|---|
| 4 | 8153 |
|---|
| 5 | 15853 |
|---|
| 6 | 38951 |
|---|
| 7 | 50138 |
|---|
| 8 | 62048 |
|---|
| 9 | 65948 |
|---|
| 10 | 54328 |
|---|
| 11 | 97552 |
|---|
| 12 | 54430 |
|---|
| 13 | 56710 |
|---|
| 14 | 40568 |
|---|
|
| 15 | 62284 |
|---|
| 16 | 36776 |
|---|
| 17 | 38680 |
|---|
| 18 | 11468 |
|---|
| 19 | 19620 |
|---|
| 20 | 14992 |
|---|
| 21 | 10360 |
|---|
| 22 | 5756 |
|---|
| 23 | 10948 |
|---|
| 24 | 25360 |
|---|
| 25 | 20720 |
|---|
| 26 | 11480 |
|---|
| 27 | 19592 |
|---|
| 28 | 9248 |
|---|
| Total | 844992
= 326*36*36*2 |
|---|
|
| 0 | 1 |
|---|
| 1 | 7 |
|---|
| 2 | 17 |
|---|
| 3 | 44 |
|---|
| 4 | 117 |
|---|
| 5 | 229 |
|---|
| 6 | 367 |
|---|
| 7 | 354 |
|---|
| 8 | 356 |
|---|
| 9 | 356 |
|---|
| 10 | 280 |
|---|
| 11 | 280 |
|---|
| 12 | 254 |
|---|
| 13 | 206 |
|---|
|
| 14 | 240 |
|---|
| 15 | 156 |
|---|
| 16 | 88 |
|---|
| 17 | 72 |
|---|
| 18 | 60 |
|---|
| 19 | 52 |
|---|
| 20 | 48 |
|---|
| 21 | 48 |
|---|
| 22 | 76 |
|---|
| 23 | 100 |
|---|
| 24 | 96 |
|---|
| 25 | 64 |
|---|
| 26 | 56 |
|---|
| 27 | 8 |
|---|
| Total | 4032
= 2016*2 |
|---|
|
| 0 | 1 |
|---|
| 1 | 16 |
|---|
| 2 | 65 |
|---|
| 3 | 116 |
|---|
| 4 | 106 |
|---|
| 5 | 76 |
|---|
| 6 | 78 |
|---|
| 7 | 62 |
|---|
| 8 | 28 |
|---|
| 9 | 16 |
|---|
| 10 | 16 |
|---|
| 11 | 24 |
|---|
| 12 | 32 |
|---|
| 13 | 16 |
|---|
| Total | 652
= 326*2 |
|---|
|
Links to other useful pages:
Mefferts. Uwe Meffert manufactures Nautilus, and you can order the puzzle on his site.
Notation:
A twist of the right hand side of the puzzle will be denoted by a slash /.
A clockwise turn of the top layer by less than a half turn to the next
twistable arrangement is denoted by U. Similarly an anti-clockwise turn of the
top layer is U'. A half turn of the top layer, regardless of whether there are any
intermediate twistable states is denoted by U2.
In the same way, a clockwise turn, half turn, and anti-clockwise turn of the
bottom layer are denoted by D, D2, and D' respectively.
Solution:
- Hold the puzzle so that the middle layers big red section is at the front-left,
with the green or orange piece at the front-right. The middle layer seam lies between
them.
- Do whatever moves are necessary to bring the two largest (red) pieces together,
side by side in the same layer. This can always be done in no more than 4 twists,
but usually in one or two. You have to manoeuvre the two red pieces so that they
are in different layers, one at the front and one at the back, and on opposite sides
of the seam, so that a twist will bring them together. This is fairly easy and
tends to happen automatically when doing random moves.
- Put the two big red pieces in the left half of the bottom layer. This keeps them out
of the way allowing you to work on the rest using twists and top layer turns only.
- Without disturbing the big red pieces, do whatever moves are necessary to place the two
smallest pieces (purple) in the top right half, one at the front directly to the right of
the seam, the other at the back directly to the right of the seam. In exceptional cases, this
can take up to 7 twists, but is usually much less. Usually just doing random twists and top
layer turns suffice to bring the two purple pieces to the top layer, the right distance apart
for a top layer turn to put them both directly to the right of the seam.
- Do a twist move to place the two small purple pieces adjacent to the two big red pieces.
- Rotate the top layer so that a yellow or a green pair of pieces is at the front,
straddling the seam, and do the same with bottom layer red pair. There are only 8 possible
positions that the puzzle can now have. Look up this position in the table below, and do
the indicated move sequence to solve the outer layers.
- If the middle layer is not yet solved, you can flip the right-hand side of the middle
layer, by doing U2 / U2 / U2 /.
Here is a table with the finishing sequences for the eight goal positions. The number in the final column
is the number of twistable positions with the reds adjacent to each other from which that goal
position can be reached without splitting the reds. It gives a rough measure of how likely each goal
position is to occur.
| 1 | 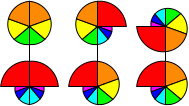 | | / U2 | 132 |
|---|
| 2 | 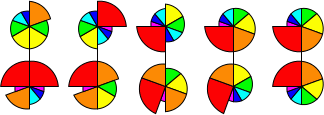 | | / U2 D' / D | 6 |
|---|
| 3 |  | | / U' / U' | 6 |
|---|
| 4 | 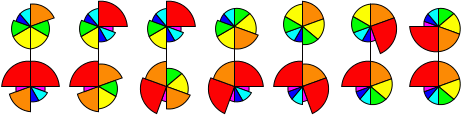 | | / D' / U' D / U | 24 |
|---|
| 5 | 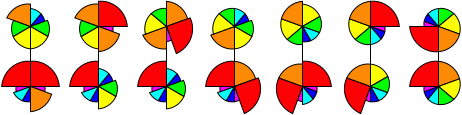 | | / U' / U D' / U2 D | 24 |
|---|
| 6 | 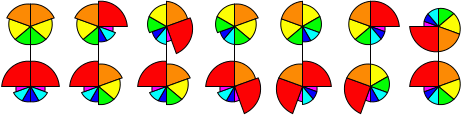 | | / U / U' D' / U2 D | 6 |
|---|
| 7 | 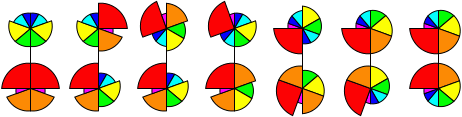 | | / U' / U' D' / D | 6 |
|---|
| 8 |  | | / D / U D' / U' D / U2 D | 6 |
|---|