Jaap's Puzzle Page

Izzi 2

Izzi 2

Izzi 2 is a tiling puzzle made in 1993 by Binary Arts (now called ThinkFun). Like the original Izzi, it was designed by Frank Nichols. Each tile is diamond shaped, and the four edges have different colours. Every tile uses the same four colours (red, yellow, blue, green) in a different order, and every possible order is represented leading to 12 tiles (4! orderings, divided by 2 because of the 180 degree symmetry of the tile shape).

Izzi 2, tile set

The booklet coming with the puzzle shows 39 different shapes. The aim of the puzzle is to put the tiles into such a shape while making sure that all the touching tile edges match in colour.

1.
Izzi 2, problem shape 1
2.
Izzi 2, problem shape 2
3.
Izzi 2, problem shape 3
4.
Izzi 2, problem shape 4
5.
Izzi 2, problem shape 5
6.
Izzi 2, problem shape 6
7.
Izzi 2, problem shape 7
8.
Izzi 2, problem shape 8
9.
Izzi 2, problem shape 9
10.
Izzi 2, problem shape 10
11.
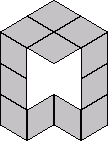
Izzi 2, problem shape 11
12.
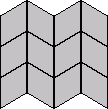
Izzi 2, problem shape 12
13.
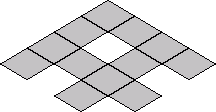
Izzi 2, problem shape 13
14.
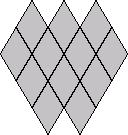
Izzi 2, problem shape 14
15.
Izzi 2, problem shape 15
16.
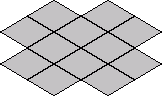
Izzi 2, problem shape 16
17.
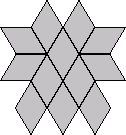
Izzi 2, problem shape 17
18.
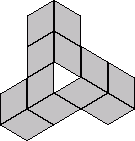
Izzi 2, problem shape 18
19.
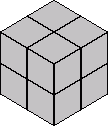
Izzi 2, problem shape 19
20.
Izzi 2, problem shape 20
21.
Izzi 2, problem shape 21
22.
Izzi 2, problem shape 22
23.
Izzi 2, problem shape 23
24.
Izzi 2, problem shape 24
25.
Izzi 2, problem shape 25
26.
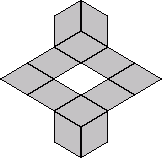
Izzi 2, problem shape 26
27.
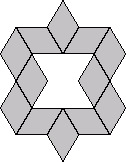
Izzi 2, problem shape 27
28.
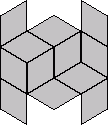
Izzi 2, problem shape 28
29.
Izzi 2, problem shape 29
30.
Izzi 2, problem shape 30
31.
Izzi 2, problem shape 31
32.
Izzi 2, problem shape 32
33.
Izzi 2, problem shape 33
34.
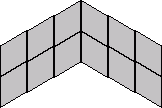
Izzi 2, problem shape 34
35.
Izzi 2, problem shape 35
36.
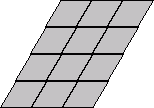
Izzi 2, problem shape 36
37.
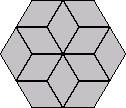
Izzi 2, problem shape 37
38.
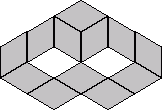
Izzi 2, problem shape 38
39.
Izzi 2, problem shape 39

The number of positions:

Thw number of ways to place 24 tiles, each with 2 possible orientations, into a given pattern is 24!·224 = 10,409,396,852,733,332,453,861,621,760,000. This is not a valid measure of difficulty, as it does not take into account that you would not try to complete a pattern after some tiles have placed that don't match. It also is the same for all the patterns above, even though they have very different difficulty levels. A better way is to simply count the number of solutions. In a pattern with many solutions it is likely to be easier to find a solution. If the patterns are ordered from most to least solutions (i.e. approximately easiest to hardest), we get the following list:
27, 15, 10, 8, 21, 29, 13, 1, 2, 30, 23, 38, 7, 25, 11, 9, 4, 35, 34, 31, 28, 17, 20, 26, 12, 18, 33, 3, 39, 37, 32 & 22, 5, 14, 16, 36, and 24 & 19 & 6.

Links to other useful pages:

ThinkFun homepage, the current name of the manufacturer Binary Arts.

Solutions:

The tiles form a complete set (i.e. every possible colour combination occurs exactly once) so if you have a solution, any permutation of the colours can be applied to create another solution. Even if you ignore such colour permutations, and any symmetry of the problem shape, all the problems have several solutions. In the table below, the colour permutation is taken into account in the number of solutions shown, but the symmetry of the shape is not.
Number of solutionsExample solutionRemarks
12504Izzi 2, Solution 1
22312Izzi 2, Solution 2
3 160Izzi 2, Solution 3
4 520Izzi 2, Solution 4
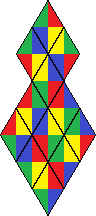5 32Izzi 2, Solution 5
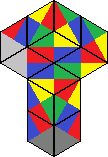6 8Izzi 2, Solution 6Only 4 essentially different solutions, all shown here.
7 952Izzi 2, Solution 7
83408Izzi 2, Solution 8
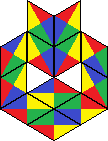9 652Izzi 2, Solution 9
104136Izzi 2, Solution 10
11 928Izzi 2, Solution 11
12 198Izzi 2, Solution 12
132616Izzi 2, Solution 13
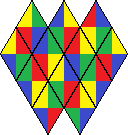14 26Izzi 2, Solution 14
154256Izzi 2, Solution 15
16 24Izzi 2, Solution 16Only 8 essentially different solutions, the 6 shown here, plus the last two "rotated" by 90 degrees.
17 272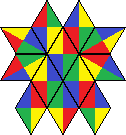Izzi 2, Solution 17
18 196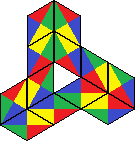Izzi 2, Solution 18
19 8Izzi 2, Solution 19Only 2 essentially different solutions, both shown here.
20 224Izzi 2, Solution 20
213128Izzi 2, Solution 21
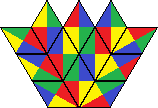22 52Izzi 2, Solution 22
231240Izzi 2, Solution 23
24 8Izzi 2, Solution 24Only 4 essentially different solutions, all shown here.
25 936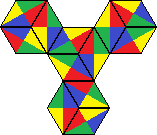Izzi 2, Solution 25
26 204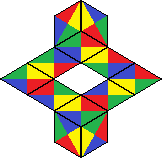Izzi 2, Solution 26
276200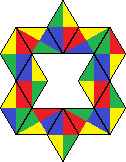Izzi 2, Solution 27
28 348Izzi 2, Solution 28
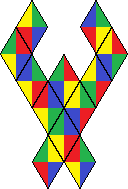292796Izzi 2, Solution 29
302276Izzi 2, Solution 30
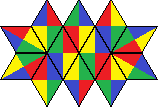31 448Izzi 2, Solution 31
32 52Izzi 2, Solution 32
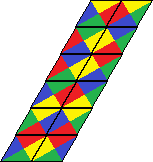33 176Izzi 2, Solution 33
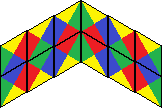34 482Izzi 2, Solution 34
35 484Izzi 2, Solution 35
36 16Izzi 2, Solution 36Only 8 essentially different solutions, the 4 shown here, and these in "mirror image".
37 66Izzi 2, Solution 37Only 11 essentially different solutions, all shown here.
381178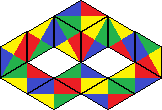Izzi 2, Solution 38
39 124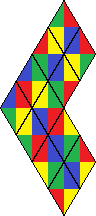Izzi 2, Solution 39