Jaap's Puzzle Page

Crossover

Crossover

Crossover is a rare sliding piece puzzle made by Nintendo. The frame has a window that shows an arrangement of 16 tiles in a 4×4 square. Each row and each column has a slider in it that allows you to slide the row or column back and forth by one tile. Every slider actually contains 5 tiles, so whenever you do a move one tile is revealed and another becomes hidden. There are 24 tiles all together - 16 visible tiles and 8 hidden at the ends of the 8 sliders.

The most unusual feature of this puzzle is that the tiles and the transparent cover are polarised in such a way that a tile looks either dark green or light grey, and that its colour changes whenever it is moved. So whenever you slide a row or column, every tile that remains visible in that column will change from dark to light or vice versa. The aim is to make all tiles dark or all tiles light. There is a version with red tiles instead of green.

The puzzle is somewhat similar to the Uriblock / Mix Box and Tsukuda's Square (a.k.a 'It'). The puzzle is mentioned in Cubic Circular Issue 2, p9.

The number of positions:

Each slider has two possible locations, so there are 28 arrangements of the sliders. There are 24 tiles, so for any state of the sliders there are at most 24! tile arrangements. This limit is not reached because there are only two types of tiles, 12 of each polarisation. This gives 24! / 12!2 = 2,704,156 tile arrangements. Combining this we get a total of 28 · 24! / 12!2 = 692,263,936 positions. All these positions can be attained.

A computer search gave the following result:
MovesPositions
01
18
244
3232
41,145
55,214
622,111
787,396
8319,035
91,063,838
103,204,222
118,578,184
1220,055,596
1340,122,924
1467,202,379
1592,827,206
16105,949,864
MovesPositions
17102,077,716
1885,639,394
1964,196,842
2043,608,330
2127,070,010
2215,446,867
238,100,732
243,897,931
251,722,226
26697,820
27257,894
2883,481
2921,156
303,730
31390
3218
Total:692,263,936

This shows that any position can be solved in at most 32 moves, where a move is sliding a single row or column and on average the optimal solution takes 16.6962 moves.

Solution:

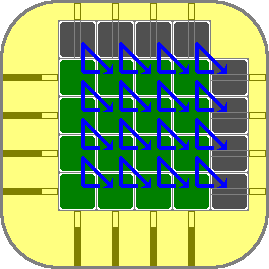
Suppose you slide a row, then a column, then slide the row back, and finally slide the column back. The effect of such a manoeuvre is that three tiles have been swapped around. The affected tiles are the one at the intersection of the column and row, and the adjacent tiles that are moved into that intersection. The picture on the right shows all possible 3-cycles that occur this way. To move the three tiles of a particular triangle in the picture, just alternately move the row and column that lie along the triangle sides.

The picture on the right shows how the colours of the three tiles will change when you perform a 3-cycle. Note that a checkerboard arrangment of colours means that the three tiles are of the same type, and so switching them around will change nothing. Another thing to notice is that the number of dark squares does not change parity, i.e. it remains odd (1 or 3) or remains even (0 or 2).

With the above insight, it becomes fairly easy to solve the puzzle. Here is general description of the order in which I solve the puzzle.

  1. Push all the columns upwards, and all the rows to the right.
  2. Solve the fourth (bottom) row from left to right.
  3. The hidden tile on the right of the fourth row should be such that when you slide the row to the left all its tiles have the same colour. If this is not the case, then fix it as follows:
    1. Solve the fourth tile in the third row, i.e. make it the same colour as the tile below it.
    2. Cycle the three tiles (rightmost tiles of third and fourth rows, hidden tile of fourth row) until the fourth row including the hidden tile is completely correct.
  4. Solve the third row, from left to right in the same way, including the hidden tile.
  5. Solve the second row, from left to right in the same way, including the hidden tile.
  6. Solve the first tile of the first row.
  7. Solve the hidden tile above the first column. It should be such that when you slide the first column down, all its tiles have the same colour. If that is not the case, then
    1. Solve the second tile in the first row, i.e. make it the same colour as the first tile of the row.
    2. Cycle the three tiles (first two tiles of the top row, hidden tile above the first column) until the first column including the hidden tile is completely correct.
  8. Solve the second tile of the top row, as well as the hidden tile above it, in the same way.
  9. Solve the third tile of the top row, as well as the hidden tile above it, in the same way.
  10. The last tile of the top row and the two hidden tiles next to it can be cycled around until they are all correct.