Solution to Atomic Chaos:

Hold the puzzle flat, with the tubes pointing to the left and right. This way you can easily tilt the puzzle to bring the balls to either half while still keeping everything clearly in view.

I will number the half-tubes from 1 to 6 according to their lengths, i.e. right tube 1 is the shortest tube in the right hand half of the puzzle, and left tube 6 is the longest tube in the left hand half of the puzzle.

All during the solutions below, the balls will all be in the right hand half of the puzzle, except of course when you are in the middle of a sequence of moves. I will therefore also assume that you start with all the balls on the right hand side. If this is not the case. just tilt the puzzle to the right, and twist the left half through a full circle, until all its balls have found the gaps on the right.

Solution 1:

This simple solution was devised by Bram Cohen. It uses only one kind of move sequence throughout, which I will describe first.

The move sequence:

1. Move empty left tubes so that left tube 6 (the longest) is joined with right tube 1 (the shortest).
2. Tilt the balls into the left half.
3. Turn the right half four steps so that one by one the balls in right tubes 2, 3, 4 and 5 drop into left tube 6. In this example we stopped with right tube 5 so that the one ball in right tube 6 remains, but another number of steps can (and will) be used as well.
4. Turn the right half back again in the opposite direction, so that once again right tube 1 is joined to left tube 6.
5. Tilt the balls into the right half.
6. Turn the left half four steps so that all the balls in left tube 6 are placed one by one in right tubes 2, 3, 4 and 5.
7. Optionally, turn the left half back, so that left tube 6 is again joined to right tube 1.

The effect of the move in this example is that the bottom balls of the first 5 right tubes are skimmed off and placed in reverse order on top. In particular, the bottom ball of tube 5 moves to tube 1, the ball in tube 1 moves to the top of tube 5, and the rest of the balls in tube 5 are shifted down. This is illustrated in the diagram on the right. The balls in the tubes between 1 and 5 are affected, but tube 6 is not.
In this example the move was applied to tube 5 because in step c the ball in right tube 5 was the last one dropped in left tube 6. Of course, if in that step you stop turning at a different right tube, then that tube will be affected instead. It is important to understand the effect of the move when applied to different tubes.

Phase 1: Solve tube 6 (Red)

1. If the ball in right tube 1 belongs in tube 6, then skip to step d.
2. Find a ball that belongs in tube 6, but which lies in a different tube. Preferably choose one that is nearest the bottom of a tube.
3. Apply the move to the tube with that ball until it moves from the bottom of its tube to tube 1.
4. Apply the move to tube 6 to drop the ball into the top of tube 6.
5. Repeat steps a-d until tube 6 is solved.

Phase 2: Solve tube 5 (Green)
This phase is nearly the same as the previous phase.

1. If the ball in right tube 1 belongs in tube 5, then skip to step d.
2. Find a ball that belongs in tube 5, but which lies in a different tube. Preferably choose one that is nearest the bottom of a tube.
3. Apply the move to the tube with that ball until it moves from the bottom of its tube to tube 1.
4. Apply the move to tube 5 to drop the ball into the top of tube 5.
5. Repeat steps a-d until tube 5 is solved.

Phase 3: Solve tubes 4, 3, and 2.
Note that phase 2 is exactly the same as phase 1 except that it was applied to a different tube, and that it didn't affect the already solved tube 6. Solving the rest of the tubes (in order from long to short) is done in exactly the same way.

Solution 2:

This is my own solution which I devised before I knew of the solution above. This solution is far more complicated, but it is useful to know its moves in order to do shortcuts or to rescue things when you make a mistake when applying the other solution. This method uses two very similar move sequences constantly throughout, so I will describe these only once.

Move sequence A:

1. Move empty left tubes 6 and 1 are joined to the right tubes 3 and 4. (This sequence will also work with the right tubes 2 and 3, or with 1 and 2 etc, but more of this later.)
2. Tilt the balls into the left half.
3. Turn the right half one step to bring right tube 4 is joined to left tube 6, dropping its remaining balls into the left half.
4. Turn the right half back again, so that right tube 4 is joined to left tube 1.
5. Tilt the balls back into the right half.
6. Turn the left half one step to join left tube 6 to right tube 4, dropping its remaining balls into the right half.
7. Optionally, turn the left half back again, so that left tube 6 is joined to right tube 3.

This move sequence only rearranges the balls in the tubes 3 and 4. Its effect on the balls is as follows:

1. The balls of tube 3 goes to the innermost positions of tube 4.
2. The 3 outer balls of tube 4 move into tube 3
3. The innermost ball of tube 4 moves to the outermost position of tube 4.

As it is described here, I'll call this move sequence A34, but it can just as well be applied to right tubes 2 and 3, which I'll call A23, or 1 and 2 (which is obviously A12). All of these have similar effects on the balls. The sequence A45 will not be used in the solution, as it has a rather complicated and not very useful effect on the balls. The move sequence A56 is useful however, and it has this effect:

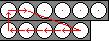
1. The innermost ball of tube 5 moves to the innermost position of tube 6.
2. The other balls of tube 5 shift inwards one step.
3. The innermost ball of tube 6 moves to the second position of tube 6.
4. The second ball of tube 6 moves to the outermost position of tube 5.

We still need a way to manipulate the balls of tube 6, and for this we use the following moves.

Move sequence B:

1. Join empty left tubes 5 and 6 to the right tubes 6 and 1.
2. Tilt the balls into the left half.
3. Turn the right half one step to join right tube 6 to left tube 6, dropping its remaining ball into the left half.
4. Turn the right half back again, so that right tube 6 is joined to left tube 5.
5. Tilt the balls back into the right half.
6. Turn the left half one step to join left tube 6 to right tube 6, dropping its remaining ball into the right half.
7. Optionally, turn the left half back again, so that left tube 6 is joined to right tube 1.

This move sequence only rearranges the balls in the tubes 6 and 1, and its effect on the balls is as follows:

1. The outermost ball of tube 6 goes to tube 1.
2. The other balls of tube 6 shift outwards one step.
3. The ball of tube 1 goes to the innermost position of tube 6.

The move sequences B, A12, A23, A34, and A56 are sufficient to solve the puzzle.

Phase 1: Solve tube 4 (Yellow)

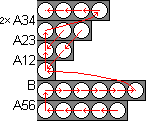1. Find a ball that belongs in tube 4, but which lies in a different tube.
2. Bring this ball to one of the innermost positions as follows:
   If it is inside tube 1, then it is already at the innermost position.
   If it is inside tube 2, do A12.
   If it is inside tube 3, do A23.
   If it is inside tube 5, do A56.
   If it is inside tube 6, do B.
   Repeat this step, until the ball is in the innermost position of any tube.
3. Now bring this ball to the innermost position of tube 3:
   If it is inside tube 1, do A12.
   If it is inside tube 2, do A23.
   If it is inside tube 3, do nothing.
   If it is inside tube 5, do A56.
   If it is inside tube 6, do B six times.
   Repeat this step, until the ball is in tube 3.
4. Finally bring the ball to the end of tube 4 by performing A34 twice. This also leaves intact any previously solved balls in tube 4.
5. Repeat steps a-d until tube 4 is solved.

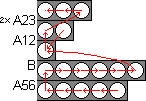Phase 2: Solve tube 3

1. Find a ball that belongs in tube 3, but which lies in a different tube.
2. Bring this ball to one of the innermost positions in the same way as step 1b.
3. Now bring this ball to the innermost position of tube 2, in a similar way as step 1c.
4. Finally bring the ball to the end of tube 3 by performing A23 twice.
5. Repeat steps a-d until tube 3 is solved.

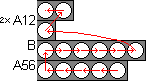Phase 3: Solve tube 2
This is done using exactly the same method as phases 1 and 2, except that you use A12 twice to move a ball from tube 1 into position in tube 2.

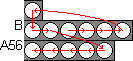Phase 4: Solve tube 5

1. Find a ball that belongs in tube 5, but which lies in a different tube.
2. Bring this ball to the second position of tube 6, by repeatedly doing sequence B.
3. Then bring the ball to the end of tube 5 by performing A56.
4. Repeat steps a-c until tube 5 is solved.

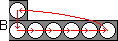Phase 5: Solve tubes 1 and 6.

1. Repeat move B until tubes 1 and 6 are solved.