





The Brain-chek puzzles consist of a 5x4 square grid, and a slider that can move along the edges of that grid. Each square has a dial, spot or other marker that changes whenever the slider moves along an edge of that square.
There are several versions. The markers of the Stoplight version (pictured above left) are pictures of stoplights which obviously have 3 states, red, yellow, green. A move along an edge of a stoplight in the clockwise direction will make it change its colour from red to green, green to yellow, or yellow back to red. A move in the opposite direction changes the light the other way. The aim is of course to make all the lights green (or all red), preferably ending with the slider at a corner.
The PhD version, pictured above middle, has both arrows and dots. The arrows have three states, and turn one step in the same direction as the direction you move the slider along an edge, similar to the Stoplight version. The dot in the centre only has two states (white or green in the picture), and changes with every move along the square's edge. Combined, the arrow and dot give each square six states.
There are also versions with just the dots, either with pictures eyes that open or close, or of faces with noses that change colour.
Lastly, there is a version where you can select the difficulty by choosing one of three sliders - one slider changes only dots, another only arrows, the third changes both. The sliders are stored in little compartements at the top of the puzzle, and can be inserted onto the grid by removing a small piece of the bottom edge of the frame.
This puzzle is a remarkable piece of mechanical design. There is a clever mechanism that locks the arrows/dots in place, and which is only released when the slider passes by. This ensures that the arrows/dots are never dislodged unintentionally.
Steven Kunreuther is the inventor/designer of the puzzle. It has taken him a long time to market it, so many of the variants of this puzzle that have found their way into puzzle collectors' hands are from relatively small prototype batches that were produced in order to promote it to puzzle manufacturers and distributors. The version with three sliders of varying difficulty has been produced in Taiwan under the name Magic Path by Getin Fun Creativity Co.
There is some interesting mathematics behind this puzzle. There is an explanation of it after the solution below. [Skip to the maths section.]
If your browser supports JavaScript, then you can play Brain-chek by clicking the link below:
| Puzzle Name | Positions | ||
| Blinking Eye | 30·220 | = | 31,457,280 |
| Stoplight | 30·320 | = | 104,603,532,030 |
| PhD | 30·620 | = | 109,684,753,201,889,280 |
Note that step f is the only one where the slider goes along the top edges of the grid.
Here are the tables for the different versions:
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Alternatively, below I have made pictures that show circuits that change only one bottom row marker.
 |
 |
 |
 |
 |
 |
 |
 |
If you can solve the 2-state and the 3-state versions of the puzzle, then you can also solve the 6-state PhD puzzle. Simply solve the arrows first just like the 3-state puzzle. Then solve the dots just like the 2-state puzzle except that you do everything 3 times so that the arrows are not affected.
The mathematics behind this puzzle is very similar to Lights Out. There are three key insights that are needed in order to fully analyse the game.
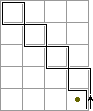
In the example below, the slider goes clockwise around one square, and then clockwise around the square to its left. The same effect is achieved by going around the left square first.

As you can see in the previous example, going around two adjacent squares one by one in the same direction has the same effect as going once around their combined 1x2 rectangle. Similarly, going around any area has the same effect as going around each square individually. All the internal edges are traversed in both directions and so their effects cancel out, leaving only the effect of travelling around the outermost path.
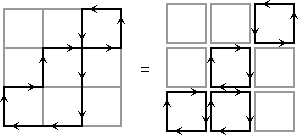
Simply move the slider towards any part of the circuit by any route, go around the circuit, and then take the same route back. This leaves the slider in the same position, the effects of the route to and fro cancel each other, so the only change is that the markers have been affected by the circuit itself.
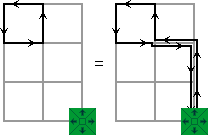
From 1 and 2 it follows that we can solve the puzzle by Linear Algebra in the same way as Lights Out. Simply consider a clockwise circuit around a single square to be one move, the equivalent of a button press in Lights Out. Such a move advances its own marker 4 times, and sets back all the adjacent markers once. We could set up a matrix of how each move affects the markers, and then invert it to get a matrix showing which moves to do to affect each marker individually. From 3 above it follows that we can do that solution regardless of what these moves are and where the slider is. So we can solve the puzzle by first moving the slider to its final spot, then calculating the solution by a matrix multiplication, and finally applying that solution by circumnavigating each square the number of times given by the solution.
The 'Light Chasing' technique that is used in Lights Out is very effective here too, as seen in the solution described above. We can solve any row of markers by doing circuits around the squares in the row below them. This allows us to reduce the size of the matrix to 4x4, and its inverse is what is used in the tables of the solution.
Once a solution is found, there is a further question to be answered. What is the best way to apply that solution?
It is nearly always inefficient to move along an edge in one direction and later move along that same edge in the other direction, as it is often possible to rearrange the order in which you do the moves to make this unnecessary. The only exception is when the solution would otherwise consist of disjoint circuits.
Also, if a marker has N possible states then going clockwise k times around a circuit has the same effect as going N-k times around anti-clockwise. Therefore you can often reduce the length of the solution by going around some squares in the other direction.
In general it is not clear to me if there is a really quick way to know for sure whether a solution path is as short as possible. Things are simpler in the case where each marker has only two states. The direction in which the slider moves along an edge doesn't matter, both directions have the same effect. The resulting graph can therefore be assumed to be undirected. All double edges can be removed, and only if that leaves a disconnected graph add the minimal amount of double edges needed to make it connected again. After all this, any Eulerian path (path that uses up all the edges of the graph exactly once) will be an optimal solution.