This wooden puzzle by Clever Toys has three separate circular tracks arranged in a triangle. The tracks contain ten coloured balls each. The balls can slide along the tracks so each ring can rotate. In the centre of the puzzle is a disc, that can rotate. Each track goes partially through the disc, so when the disc is rotated four balls of each ring get moved to the next ring. Solving the puzzle is made more difficult by the fact that in each ring two pairs of balls are joined together. If such a double piece lies across the seam that separates the middle disc from the rest, the disc cannot move.
The balls come in three colours. In its solved state every ring is a single colour. Furthermore, the bandaged pieces in a ring should be on opposing sides, with three single balls between them on either side.
This puzzle should not be confused with another puzzle of the same name, which you can see on the Turnstile / Puzzler page.
Let's count the number of arrangements the bandaged pairs can have. The six pieces can be arranged amongst the rings in the several ways, and the table below tallies them systematically.
| Distribution amongst rings | Arrangements per ring | Total | |
|---|---|---|---|
| 0+1+5, 0+5+1, 1+0+5, 1+5+0, 5+0+1, 5+1+0 | 1, 10, 2 | 6·1·10·2 = | 120 |
| 0+2+4, 0+4+2, 2+0+4, 2+4+0, 4+0+2, 4+2+0 | 1, 35, 25 | 6·1·35·25 = | 5,250 |
| 0+3+3, 3+0+3, 3+3+0 | 1, 50, 50 | 3·1·50·50 = | 7,500 |
| 1+1+4, 1+4+1, 4+1+1 | 10, 10, 25 | 3·10·10·25 = | 7,500 |
| 1+2+3, 1+3+2, 2+1+3, 2+3+1, 3+1+2, 3+2+1 | 10, 35, 50 | 6·10·35·50 = | 105,000 |
| 2+2+2 | 35, 35, 35 | 1·35·35·35 = | 42,875 |
| 168,245 | |||
Given any one of these 168,245 arrangements, we now have to count in how many ways we can assign the colours to the pieces. The 6 bandaged pieces have 2 of each colour, so can have 6!/2!3 colour patterns. The 18 single balls have 6 of each colour, and hence 18!/6!3 colour patterns. Combining all these numbers we get a grand total of 168245·6!/2!3·18!/6!3 = 259,733,642,968,800 positions. Note that this is a slight overestimate. Some positions have one or more rings with a repeating arrangement and colour pattern. The solved position for example remains unchanged if any ring is given a half turn, so it is counted 2·2·2 times in our total. The vast majority of positions do not have such symmetry, so the number is pretty accurate.
A clockwise shift of the upper, left, or right ring by one ball will be denoted by the letters U, L, and R respectively. Anti-clockwise shifts have the letter followed by an apostrophe, i.e. they are denoted by U', L', and R'. Similarly rotations of the middle disc are denoted by M and M'.
Phase 1: Arrange the double pieces.
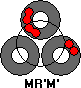If there are is a ring with two adjacent double pieces, then:
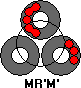If there are is a ring that has two double pieces with a single ball between them, then:
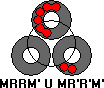If there are is a ring that has two double pieces with exactly two single balls between them, then:
Phase 2: Solve the double pieces.
In this phase use only half turns of the rings so that the arrangement of the pieces will remain the same.
Phase 3: Solve the single balls.
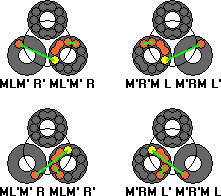Find two unsolved balls that you wish to swap, at least one of which should be next to a double piece.
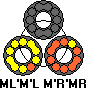The only case left is when none of the incorrect balls are adjacent to a double piece. Choose two of the incorrect balls that you want to swap.