Thistlethwaite's 52-move algorithm
Morwen B. Thistlethwaite is a mathematician who devised a clever algorithm
for solving the Rubik's Cube in remarkably few moves.
It is a rather complicated method, and therefore cannot be memorised. It is only
practical for computers and not for humans. This algorithm is rather important from
a theoretical standpoint however, as it has long been the method with the fewest
number of moves.
Thistlethwaite's method differs from layer algorithms and corners first
algorithms in that it does not place pieces in their correct positions one by
one. Instead it works on all the pieces at the same time, restricting them to
fewer and fewer possibilities until there is only one possible position left
for each piece and the cube is solved.
The way it does this is by first doing a few moves until a position arises
that can be solved without using quarter turns of the U and D faces (though
half turns of U and D are still needed). It then proceeds to solve the cube
without using U or D quarter turns by first moving to a position that does not need
quarter turns of the F, B faces either. With these further restrictions a position
is arrived at that does not need any quarter turns at all, and can hence be solved
by half turns only. The cube then indeed gets solved using half turns only.
These four stages are quite complicated, since they use large look-up tables
for all the positions at each stage. The table below shows the numbers
involved:
| Group | # positions | Factor |
|---|
| G0=<L, R, F, B, U, D> | 4.33·1019 | | |
| | 2,048 | (211) |
| G1=<L, R, F, B, U2,D2> | 2.11·1016 | | |
| | 1,082,565 | (12C4 ·37) |
| G2=<L, R, F2,B2,U2,D2> | 1.95·1010 | | |
| | 29,400 | ( 8C42 ·2·3) |
| G3=<L2,R2,F2,B2,U2,D2> | 6.63·105 | | |
| | 663,552 | (4!5/12) |
| G4=I | 1 | | |
Mathematically speaking, this is a sequence of nested groups, and each
stage of the algorithm is simply a look-up table showing a solution for
each element in the quotient coset space. The last column shows the order
of these coset spaces, i.e. the size of the look-up tables used.
The first stage has a factor of 2,048=211. This corresponds to the fact
that this stage fixes the orientation of the edges; it is impossible to
flip edges if only half turns are allowed on the U, D faces, but otherwise
the pieces can be put in any normal position with this restriction.
The second stage has a factor of 37 *12!/(8!4!). This corresponds to the
fact that this stage fixes the orientation of the corners, and places the
middle layer edges into their slice. It is fairly easy to see that if you
are only allowed half turns on the F,B,U,D faces together with any turns on the L, R
faces, then the left and right faces will never have more than two colours,
and the middle edge pieces will never leave their slice or be flipped.
In fact, those restricted moves can solve any position under those
conditions.
The third stage has a factor of [8!/(4!4!)]2 *2*3. This corresponds to the
fact that the edges in the L and R faces are placed in their correct
slices, the corners are put into their correct tetrads, the parity of the
edge permutation (and hence the corners too) is made even, and the total
twist of each tetrad is fixed.
The final stage finally solves the cube.
The following table shows the number of moves each stage needs.
| 1 | 2 | 3 | 4 | Total |
|---|
| Original algorithm: | 7 | 13 | 15 | 17 | 52 |
|---|
| Improved algorithm: | 7 | 13 | 15 | 15 | 50 |
|---|
| Best possible: | 7 | 10 | 13 | 15 | 45 |
|---|
To keep the size of the lookup tables down, Thistlethwaite used
simplifying preliminary moves which is why the number of moves he needed is
sometimes more than the best possible (the 'diameter' of the quotient spaces).
His students first improved the algorithm by completely analysing the square group,
thus reducing it to 50 moves. Later each stage was fully computed, for a 45 move
solution. In 1991 Hans Kloosterman reduced that to 42 moves by using slightly
different stages 3 and 4.
Through extensive calculations, Mike Reid has shown that
going from G0 directly to G2 can be done in 12 moves,
and from G2 to G4 in 18 moves. When combining these, the 30-move cases
can be avoided, so it has been proved that 29 moves is always sufficient to solve
the cube. More recently other techniques have allowed computers to verify that
God's Algorithm is 20 moves in the worst case.
Ryan Heise
has developed a way of solving the cube based on Thistlethwaite's algorithm. He splits stages 2, 3 and
4 into two steps each (corners and edges separately) in order to make it possible for a human being to memorise.
David Singmaster has made scans of Thistlethwaite's printouts, and I converted them to
text. Below is a reproduction of those papers, as accurate as I can make them. It consists
of
1. Covering letter, 1 page
2-4. General Instructions, 3 pages
5-10. Stage 2 tables, 6 pages
11-18. Stage 3 tables, 8 pages
19-25. Stage 4 tables, 7 pages
26. Detailed example, 1 page.
Note that the hand-written corrections in the introduction are shown in italics here.
26 Queens Road,
Loughton,
Essex.
13 July 1981.
Dear
Thank you for your letter asking for a copy of my
52-move strategy for solving Rubik's Cube. Please find
enclosed the following:-
(i) General instructions and description (3 pages);
(ii) Tables for Stage 2 (computer print-out);
(iii) Instructions and table for the first part of Stage 3;
(iv) Tables for the latter part of stage 3 (7 typewritten pages);
(v) Tables for Stage 4 (7 pages of computer print-out, photocopied).
I should perhaps point out that this strategy isn't
easy to perform (even John Conway finds it quite hard!),
for two reasons: first, only one representative of each
symmetry class is given in the tables; second, I have
given only the barest documentation. I hope that a fuller
description will be forthcoming at some stage.
On reading the bottom of page 2 of the General Instructions,
you will note that in fact Stage 2 requires two sets of
tables. I have omitted to send you the second of these,
because they are bulky, and only save one move! I hope you
will excuse this liberty. One can always get FU,FD,BU,BD
into the UD-slice (the middle horizontal slice) in at
most five moves in G1.
As an example of the strategy at work, consider the
position where the four upper corners are twisted clockwise,
the four lower corners are twisted antlclockwise, and all
twelve edges are flipped. Then the cube is restored by:-
Stage 1 DBFUR'L'D
Stage 2 L2F2D2F | L2R2F'R'BR2B'R'B'
Stage 3 L2B2 | U2LU2F2L2F2L'B2LB2L'
Stage 4 R2U2 | R2D2F2U2B2D2F2B2L2B2L2B2
Yours sincerely,
Morwen B. Thistlethwaite.
page 1
THE 45-52 MOVE STRATEGY
Introduction. Let G= <L,R,F,B,U,D> , G1= <L,R,F,B,U2,D2> ,
G2= <L,R,F2,B2,U2,D2> , G3= <L2,R2,F2,B2,U2,D2> . The plan is to
manoeuvre down through the chain G=G0> G1> G2> G3> 1. One gets from
Gi to Gi+1 by using moves in Gi only. In its shortest form this
strategy would be executed with the help of a computer, in which case
I conjecture only 45 moves would be needed, but here I have sacrificed
7 moves in order that there should be no need for a computer. With a
few more pages of tables, the figure 52 could be reduced to an
intermediate figure of, say, 49. I intend to do this shortly!
The indexes of the chain of subgroups are 2048, 1082565, 29400, 663552,
but these figures are considerably reduced by considering symmetries.
The reader may check that these indexes multiply together to give the
order of G. The accompanying tables are broadly classified according to
corner positions, and in detail according to edge positions. The words
listed actually produce the positions under consideration, so the
restoring moves are the inverses of these. In order to be able to use
the tables it is necessary to understand the basic characteristics of the
groups G1, G2, G3, so the necessary facts are presented below.
Getting into G1. This involves edge pieces only, and is easy, for which
reason no tables are given. An edge piece is BAD if in taking it home an odd
number of quarter-turns of U and D faces is needed; otherwise it is GOOD
(note that badness is well-defined). The reader may quickly work out a rule of
thumb for deciding whether a piece is GOOD or BAD. Now quarter-turns of
either U or D faces convert BAD pieces to GOOD and vice versa; other moves
have no effect. Therefore to make all edge pieces GOOD, move groups of them
to U or D face avoiding quarter-turns of U or D, and then cure them by
performing a quarter-turn of U or D. For example, if all twelve are BAD,
DBFUR'L'D will cure them all!
page 2
Getting from G1 into G2. What has been achieved so far (although
it doesn't look like it) is the correct orientation of edge pieces! In
the present stage, the same is accomplished for corners, and also the
edge pieces FU, FD, BU, BD are brought into their slice. As is well
known, corners do not in general have a natural orientation, but here,
roughly speaking, we shall line them all up the same way. More precisely,
note that each corner piece has either a L-facet or a R-facet: on
completion of this stage each of these facets will lie on either the L
or the R face. In fact, the same will be true of the eight edge pieces
with L or R facets, in view of the statement above regarding FU, FD, BU, BD.
There are 1082565 cases to consider here, this number being the product of
3^7(total number of corner orientations) , and 12C4 (total number of
arrangements of the set {FU, FD, BU, BD} amongst the twelve edge positions).
Surprisingly, with a certain amount of practice it is possible to get
through this stage in at most 17 moves without tables; the same is most
certainly not true of the next stage although there are only 29400 cases.
However, with a few pages of tables this figure of 17 may be reduced to 13;
with a great deal more computation, it should be possible to reduce it
further to 10. To "prove" that 10 moves were sufficient, one would run
through all 10-move sequences on the computer, and check that 1082565 different
cases resulted. This would take no more than a few hours of computer
time, in view of certain short cuts available by considering symmetries.
Now to business. The twist of a corner is measured by looking at its
L or R facet and observing how this has been rotated in relation to the
adjacent L or R face. Note that quarter-turns of F and B faces alter the
twist of corners, whereas all other moves in the group G1 have no effect.
Now in at most 4 moves in G1 try to obtain a position where either the corners
on the F face or the corners on the B face have zero twist. Note the twist
of the corners on the opposite face and also the positiosn of the edge pieces
the edge pieces FU, FD, BU, BD are all in the UD-slice. If this is not
possible, get them all in the U-face in at most 4 moves.
page 3
FU, FB, BU, BD, and tThen refer to the appropriate detailed table. The
words listed in these tables need to be inverted, as mentioned earlier.
Getting from G2 into G3. This is the trickiest stage theoretically,
and may be broken down for purposes of clarification into two sub-stages:
first get corners into their natural orbits, and second permute the
corners within their orbits so as to obtain one of the 96 corner permutations
in the squares group (G3), while at the same time sorting out the edge
pieces into their correct slices. The table of initial moves on the first
page of Stage 3 tables does part of the first of these substages, and the
detailed tables do the rest. After performing the initial moves, the set
of corners out of orbit will be one of three possibilities (modulo symmetries):
(i) the empty set; (ii) the set {1, 8, 2, 7} ; (iii) the set {1, 5} .
The reader then has to calculate which coset of form G3αβ the permutation
of corners lies in, where α is one of 1, (14)(68), (24)(58), (12), (14), (24),
and β is one of 1, (18)(27), (15). Since some of these cosets are reflections
of others, it was not necessary to produce tables for all six possible values
of α. The task of reflecting positions if necessary is left to the reader.
I apologise for the slightly anomalous numbering of edge positions for this
stage; this was due originally to a typing error in a programs and has
stuck ever since!
Getting from G3 to home. In this final stage one uses only 180 turns.
The order of G3 is 96x6912 = 663552. The tables for this stage give words
for producing each of the 6912 edge positions with corners fixed. Therefore
one must first restore the corners (in at most 4 moves), and then use the
tables to restore the edges. Considerable practice is needed to use these
tables efficiently, but I have found (after considerable practice) that I
can find the desired move in about 2 minutes. One hint is that when faced
with three 3-cycles, consider the configuration of the fixed pieces. Also
it pays to get to know the different sorts of 4-cycle.
STAGE 2 TABLES
FIRST BATCH OF NUMBERS: THE MOVES.
11=L 12=L2 13=L'
21=F 22=F2 23=F'
31=R 32=R2 33=R'
41=B 42=B2 43=B'
51=U2 52=D2
SECOND BATCH OF NUMBERS: TWISTS OF CORNERS.
1=CLOCKWISE 2=ANTICLOCKWISE 0=NO EFFECT
FINAL NUMBER: NUMBER OF SYMMETRICALLY EQUIVALENT POSITIONS.
N.B. FOR INITIAL 1X READ 21 1X.
21 11 31 22 11 31 51 52 21 0 0 0 0 0 0 0 0 1
21 11 33 42 11 51 33 52 21 0 0 0 1 0 0 2 0 4
21 11 22 51 52 12 22 33 21 0 0 0 1 1 0 2 2 8
21 11 22 31 43 51 13 22 11 0 0 0 1 1 1 2 1 8
21 11 52 11 21 31 52 41 51 0 0 0 1 2 2 0 1 8
21 11 22 12 52 12 52 31 41 0 0 0 2 0 1 2 1 8
11 21 33 23 11 32 51 52 23 0 0 1 0 0 0 2 0 4
11 21 33 23 11 32 51 52 21 0 0 1 0 2 0 0 0 4
11 42 31 21 13 42 33 41 51 0 0 1 1 0 0 2 2 2
21 11 21 33 42 11 23 12 43 0 0 1 1 0 1 0 0 8
21 11 22 31 41 11 32 42 13 0 0 1 1 1 0 1 2 8
21 11 31 21 51 31 21 41 11 0 0 1 1 2 2 0 0 2
21 11 22 32 41 51 13 22 11 0 0 1 1 2 2 2 1 8
21 11 21 41 11 23 41 11 43 0 0 1 2 0 0 0 0 8
21 11 41 51 41 12 42 11 41 0 0 1 2 0 0 1 2 4
21 11 42 12 41 52 41 11 41 0 0 1 2 0 0 2 1 4
21 11 21 32 42 11 23 12 43 0 0 1 2 0 1 0 2 8
21 11 22 12 22 51 31 52 21 0 0 1 2 1 0 0 2 8
21 11 21 12 23 42 11 43 12 0 0 1 2 1 0 1 1 8
21 11 22 13 21 31 21 11 41 0 0 1 2 1 1 0 1 8
21 11 21 41 11 23 43 11 43 0 0 1 2 2 1 0 0 4
21 11 22 11 52 33 51 21 51 0 0 2 0 0 0 0 1 4
21 11 22 11 22 52 33 51 23 0 0 2 0 0 0 1 0 4
21 11 22 11 52 33 51 21 12 0 0 2 0 0 1 0 0 4
21 11 22 11 22 52 33 51 21 0 0 2 0 1 0 0 0 4
21 11 33 42 11 21 12 31 43 0 0 2 1 1 0 0 2 8
21 11 22 13 21 13 21 12 43 0 0 2 1 1 1 2 2 8
21 11 21 11 52 11 23 11 43 0 0 2 2 0 0 1 1 2
21 11 22 11 32 52 33 51 23 0 0 2 2 0 0 2 0 8
21 11 23 11 33 51 21 12 43 0 0 2 2 2 0 0 0 8
21 11 51 31 23 52 12 21 33 0 1 0 0 0 2 1 2 8
21 11 22 51 52 12 22 33 23 0 1 0 0 2 0 1 2 8
21 11 52 11 21 31 52 41 12 0 1 0 0 2 1 0 2 8
21 11 32 43 12 31 43 51 31 0 1 0 0 2 2 2 2 8
21 11 21 43 11 31 21 51 31 0 1 0 1 2 0 1 1 8
21 12 22 51 52 31 22 32 21 0 1 0 1 2 0 2 0 2
11 23 41 31 41 11 33 52 21 0 1 0 1 2 2 0 0 8
21 11 22 12 51 31 52 21 12 0 1 0 2 0 0 1 2 8
21 11 32 51 43 52 33 23 12 0 1 0 2 0 2 0 1 4
11 22 11 51 41 11 52 23 51 0 1 0 2 1 0 2 0 4
21 11 42 51 41 11 33 23 33 0 1 0 2 2 1 2 1 8
21 11 51 33 41 33 21 51 11 0 1 0 2 2 2 0 2 8
11 22 51 43 11 33 21 42 11 0 1 1 0 0 2 0 2 8
12 22 51 52 31 22 32 21 31 0 1 1 0 2 0 0 2 2
21 11 21 43 11 31 21 51 33 0 1 1 0 2 0 1 1 8
21 11 22 31 41 13 22 13 22 0 1 1 0 2 1 0 1 8
21 11 51 43 31 21 42 51 11 0 1 1 0 2 1 2 2 8
21 11 21 33 51 41 11 21 51 0 1 1 1 1 0 1 1 8
11 21 11 43 33 43 51 13 23 0 1 1 1 1 0 2 0 8
11 22 12 21 32 51 52 31 21 0 1 1 1 2 0 2 2 4
21 11 21 12 42 31 23 11 43 0 1 1 2 0 0 1 1 8
21 11 32 23 11 51 52 21 51 0 1 1 2 0 2 0 0 8
21 11 21 42 12 23 11 43 12 0 1 1 2 1 0 1 0 8
21 11 21 12 32 23 42 11 43 0 1 1 2 2 1 1 1 8
21 11 21 11 43 31 51 33 21 0 1 2 1 0 1 1 0 8
21 11 22 11 21 52 33 51 23 0 1 2 1 0 2 1 2 4
21 11 21 11 43 31 51 33 23 0 1 2 1 1 1 0 1 8
21 11 22 11 21 52 33 51 21 0 1 2 1 1 2 0 2 4
21 11 23 31 23 43 13 22 13 0 1 2 1 2 0 2 1 4
21 11 22 31 52 23 52 13 41 0 1 2 1 2 2 0 1 8
21 11 21 11 33 21 42 32 41 0 1 2 2 0 1 0 0 8
21 11 21 42 31 23 13 41 12 0 1 2 2 2 1 1 0 8
21 11 32 22 11 51 52 21 51 0 2 0 1 0 0 0 0 8
21 11 21 12 51 43 31 23 51 0 2 0 1 0 1 1 1 8
11 22 11 51 41 11 52 21 12 0 2 0 1 0 2 0 1 4
21 11 31 51 43 52 33 21 51 0 2 0 1 1 0 2 0 4
21 11 32 41 11 31 51 23 31 0 2 0 1 2 1 0 0 8
21 11 51 52 22 41 12 33 21 0 2 0 2 0 2 0 0 8
21 11 21 12 23 11 22 41 51 0 2 0 2 1 0 0 1 8
21 11 32 21 31 42 13 31 41 0 2 0 2 2 0 0 0 8
21 11 21 51 41 11 23 51 12 0 2 0 0 0 1 1 1 8
21 11 32 23 13 33 42 33 41 0 2 1 0 2 0 1 0 8
21 11 32 41 11 31 51 23 33 0 2 1 0 2 1 0 0 8
21 11 21 32 51 41 11 21 51 0 2 1 1 0 0 1 1 8
21 11 21 11 52 31 23 12 43 0 2 1 1 0 1 1 0 8
21 11 31 21 13 42 33 43 51 0 2 1 1 1 0 2 2 4
21 11 21 12 31 23 11 22 43 0 2 1 1 1 1 0 0 8
21 11 21 12 21 41 11 22 13 0 2 1 1 1 1 2 1 8
21 11 23 31 23 41 13 22 13 0 2 1 1 2 0 2 1 8
21 11 23 33 23 41 13 22 13 0 2 1 1 2 1 2 0 8
11 21 11 31 51 11 41 13 21 0 2 1 1 2 2 0 1 4
21 11 51 31 21 41 51 11 22 0 2 1 1 2 2 2 2 8
21 11 21 11 31 52 23 12 43 0 2 1 2 0 0 1 0 8
21 11 21 11 31 21 42 32 41 0 2 1 2 0 1 0 0 8
21 11 21 31 22 11 21 12 43 0 2 1 2 0 1 1 2 8
21 11 21 51 13 21 51 41 51 0 2 1 2 1 0 1 2 4
21 11 21 42 13 43 13 23 13 0 2 1 2 2 0 2 0 8
21 11 21 12 23 11 41 12 32 0 2 2 0 0 0 1 1 8
21 11 22 11 32 52 33 51 21 0 2 2 0 2 0 0 0 8
21 11 21 33 21 32 22 13 41 0 2 2 1 0 1 1 2 4
21 11 21 42 32 23 13 41 12 0 2 2 1 2 1 1 0 4
21 11 21 11 23 32 51 52 21 0 2 2 2 0 0 0 0 8
21 11 21 11 33 52 23 12 43 0 2 2 2 2 0 1 0 8
21 11 33 42 13 51 31 51 41 1 0 0 0 0 0 0 2 4
21 11 22 42 13 22 11 22 41 1 0 0 0 2 1 1 1 8
21 11 21 33 42 11 23 12 41 1 0 0 1 0 0 0 1 8
21 11 22 11 42 11 51 52 21 1 0 0 1 0 0 1 0 8
11 21 31 21 12 51 31 52 21 1 0 0 1 0 0 2 2 8
21 11 22 42 12 51 31 52 21 1 0 0 1 1 0 1 2 8
11 22 11 32 51 41 11 52 21 1 0 0 1 2 0 0 2 2
21 11 21 41 11 31 21 51 31 1 0 0 1 2 0 1 1 8
21 11 21 41 11 23 41 11 41 1 0 0 2 0 0 0 0 8
21 11 42 12 41 52 41 11 43 1 0 0 2 0 1 2 0 4
21 11 21 32 42 11 23 12 41 1 0 0 2 0 2 0 1 8
21 11 41 51 41 12 42 11 43 1 0 0 2 0 2 1 0 4
21 11 51 33 43 32 23 52 31 1 0 0 2 0 2 2 2 8
21 11 21 32 21 52 31 52 43 1 0 0 2 1 0 1 1 8
21 11 21 41 11 23 43 11 41 1 0 0 2 2 0 0 1 4
21 11 23 11 51 32 21 12 41 1 0 0 2 2 0 1 0 8
21 11 32 51 22 41 51 11 21 1 0 1 0 1 0 0 0 8
21 11 22 31 43 11 32 42 13 1 0 1 0 1 0 1 2 8
21 11 51 43 31 21 42 51 13 1 0 1 0 1 2 2 2 8
21 11 21 41 11 31 21 51 33 1 0 1 0 2 0 1 1 8
21 11 42 31 21 13 42 33 41 1 0 1 0 2 0 2 0 2
21 11 21 12 31 51 43 31 21 1 0 1 1 1 1 1 0 8
21 11 21 31 41 33 21 52 33 1 0 1 1 1 2 1 2 8
21 11 21 31 41 33 21 52 31 1 0 1 1 1 2 2 1 8
21 11 23 32 41 33 23 52 31 1 0 1 1 2 0 2 2 4
21 11 21 12 41 31 21 51 31 1 0 1 1 2 1 1 2 8
21 11 21 12 41 31 21 51 33 1 0 1 1 2 1 2 1 8
21 11 41 11 41 52 11 52 43 1 0 1 2 0 0 0 2 8
21 11 21 12 22 32 21 11 41 1 0 1 2 0 0 1 1 8
21 11 21 12 22 32 21 11 43 1 0 1 2 0 1 1 0 8
21 11 32 23 11 51 52 23 51 1 0 1 2 0 2 0 0 8
21 11 21 12 31 23 11 43 12 1 0 1 2 1 0 1 0 8
21 11 21 33 23 42 13 43 51 1 0 1 2 2 1 1 1 8
21 11 51 33 43 32 23 52 33 1 0 2 0 0 2 2 2 8
21 11 32 23 11 22 51 52 23 1 0 2 1 0 0 0 2 8
21 11 21 42 12 33 23 11 43 1 0 2 1 0 1 1 0 8
21 11 23 31 23 43 13 22 11 1 0 2 1 0 2 2 1 4
21 11 21 12 33 23 11 43 12 1 0 2 1 1 0 1 0 8
21 11 22 51 21 51 42 13 41 1 0 2 1 2 2 1 0 8
21 11 21 11 23 13 42 13 41 1 0 2 2 0 0 0 1 8
21 11 21 12 22 33 21 11 43 1 0 2 2 0 0 1 0 8
21 11 21 12 22 31 21 11 43 1 0 2 2 0 1 0 0 8
21 11 21 42 13 41 13 23 11 1 0 2 2 0 2 1 1 4
21 11 21 32 42 31 23 13 43 1 0 2 2 1 0 1 2 8
21 11 21 42 32 23 13 43 51 1 0 2 2 2 0 1 1 4
21 11 21 43 11 23 43 11 41 1 0 2 2 2 1 0 1 8
21 11 22 12 52 43 13 51 21 1 0 2 2 2 2 0 0 8
21 11 22 11 42 11 51 52 23 1 1 0 0 1 0 0 0 8
21 11 21 51 21 31 43 52 33 1 1 0 0 1 0 1 2 8
21 11 21 51 21 31 43 52 31 1 1 0 0 1 0 2 1 8
21 11 22 31 43 13 22 13 51 1 1 0 0 1 1 2 0 8
21 11 23 43 52 11 21 52 11 1 1 0 0 2 2 2 1 8
11 21 33 41 11 23 41 11 41 1 1 0 1 0 0 0 0 8
21 11 23 12 41 31 23 51 31 1 1 0 1 0 0 1 2 8
21 11 23 12 43 31 23 51 31 1 1 0 1 0 1 0 2 8
11 22 31 21 43 33 23 52 31 1 1 0 1 2 0 2 2 4
21 11 21 12 42 31 23 11 41 1 1 0 2 0 1 1 0 8
21 11 21 12 33 23 11 41 51 1 1 0 2 1 0 1 0 8
21 11 23 43 31 23 12 51 31 1 1 1 0 0 0 1 2 8
21 11 21 33 51 41 11 21 12 1 1 1 0 0 1 1 1 8
21 11 23 12 43 31 23 51 33 1 1 1 0 0 1 2 0 8
21 11 42 32 23 11 51 52 21 1 1 1 0 0 2 1 0 8
21 11 21 12 31 51 43 31 23 1 1 1 0 1 1 1 0 8
21 11 22 41 51 13 22 13 51 1 1 1 0 1 1 2 2 8
21 11 32 51 23 33 43 52 31 1 1 1 0 1 2 0 0 8
11 22 31 21 43 33 23 52 33 1 1 1 0 2 0 2 2 4
21 11 22 41 51 13 22 11 22 1 1 1 0 2 2 1 1 8
21 11 21 31 51 32 41 11 21 1 1 1 1 0 0 1 1 4
21 11 31 41 13 23 51 23 13 1 1 1 1 0 2 1 2 8
21 11 21 31 51 32 41 11 23 1 1 1 1 1 0 0 1 4
21 11 21 32 51 31 41 11 21 1 1 1 1 1 0 1 0 4
21 11 31 41 13 23 51 23 11 1 1 1 1 2 0 1 2 8
21 11 21 12 43 31 21 51 31 1 1 1 1 2 1 1 1 8
21 11 33 51 12 21 41 52 11 1 1 1 1 2 2 2 2 1
21 11 21 11 51 13 41 11 23 1 1 1 2 0 0 0 1 8
21 11 22 33 43 11 32 42 13 1 1 1 2 1 0 1 2 8
21 11 21 43 33 22 52 23 33 1 1 1 2 1 2 0 1 8
21 11 22 12 21 51 52 31 21 1 1 1 2 1 2 2 2 4
21 11 31 21 41 13 22 51 13 1 1 1 2 2 1 2 2 4
21 11 32 23 11 22 51 52 21 1 1 2 0 0 0 0 2 8
11 21 33 22 43 33 52 23 31 1 1 2 0 2 0 0 0 8
21 11 21 13 23 33 21 31 41 1 1 2 1 0 0 0 1 8
21 11 21 43 33 22 52 23 31 1 1 2 1 1 2 1 0 8
21 11 22 33 43 13 22 13 22 1 1 2 1 2 1 0 1 8
21 11 22 12 23 11 22 11 43 1 1 2 2 1 1 2 2 2
21 11 22 42 52 23 52 13 41 1 1 2 2 2 0 0 1 8
21 11 33 21 13 42 31 22 41 1 1 2 2 2 2 1 1 2
21 11 22 12 42 52 13 51 21 1 2 0 0 1 0 0 2 8
21 11 22 13 41 51 41 33 43 1 2 0 0 1 1 2 2 8
21 11 32 23 13 33 42 33 43 1 2 0 0 2 0 1 0 8
21 11 21 11 52 31 23 12 41 1 2 0 1 0 0 1 1 8
21 11 21 12 31 23 11 22 41 1 2 0 1 1 0 0 1 8
21 11 22 42 12 51 52 31 21 1 2 0 1 1 0 2 2 8
21 11 41 13 52 21 42 33 21 1 2 0 1 2 1 2 0 8
21 11 21 11 31 52 23 12 41 1 2 0 2 0 0 1 0 8
21 11 21 31 22 11 21 12 41 1 2 0 2 0 2 1 1 8
21 11 32 23 11 51 52 21 12 1 2 1 0 2 0 0 0 8
21 11 22 51 43 11 21 42 13 1 2 1 0 2 0 1 2 8
21 11 21 11 51 13 41 11 21 1 2 1 1 0 0 0 1 8
21 11 22 43 12 52 11 22 13 1 2 1 1 1 0 2 1 8
21 11 21 32 21 41 13 22 13 1 2 1 1 1 1 2 0 8
21 11 21 41 52 43 12 31 41 1 2 1 1 1 2 0 1 8
21 11 23 32 41 33 52 23 33 1 2 1 1 2 0 0 2 8
21 11 23 32 41 33 52 23 31 1 2 1 1 2 0 2 0 8
21 11 21 41 31 21 12 51 33 1 2 1 1 2 1 0 1 8
21 11 21 41 31 21 12 51 31 1 2 1 1 2 1 1 0 8
21 11 32 21 42 13 22 13 43 1 2 1 1 2 1 2 2 4
21 11 21 13 31 43 11 23 13 1 2 1 2 1 1 1 0 8
21 11 22 43 33 21 52 23 33 1 2 1 2 1 2 0 0 8
21 11 21 33 43 33 21 52 33 1 2 1 2 1 2 1 2 2
21 11 21 11 51 21 11 41 11 1 2 1 2 2 0 0 1 8
21 11 21 11 33 23 12 43 51 1 2 2 0 0 1 0 0 8
21 11 32 23 43 33 52 21 33 1 2 2 0 0 2 0 2 8
21 11 22 12 52 43 13 51 23 1 2 2 0 0 2 2 0 8
21 11 51 21 12 22 51 33 43 1 2 2 1 0 0 0 0 4
21 11 21 13 33 43 13 23 13 1 2 2 1 1 0 2 0 8
21 11 21 12 21 11 22 13 43 1 2 2 1 1 1 0 1 8
21 11 21 13 33 43 11 23 13 1 2 2 1 1 1 1 0 8
21 11 21 33 43 33 21 52 31 1 2 2 1 1 2 2 1 2
21 11 21 13 21 41 11 21 13 1 2 2 1 2 0 0 1 8
21 11 21 13 21 43 11 21 13 1 2 2 1 2 1 0 0 8
21 11 21 33 22 32 21 13 41 1 2 2 1 2 2 1 1 8
21 11 21 11 22 31 21 12 41 1 2 2 2 0 0 1 1 8
21 11 21 11 21 31 22 12 41 1 2 2 2 0 1 0 1 8
21 11 21 12 51 33 23 51 43 1 2 2 2 0 1 1 0 8
21 11 21 32 21 33 22 13 41 1 2 2 2 0 2 1 2 8
21 11 21 13 32 41 11 23 13 1 2 2 2 1 0 1 0 8
21 11 21 12 51 32 43 33 21 1 2 2 2 1 1 1 2 4
21 11 21 31 22 32 21 13 41 1 2 2 2 1 2 1 1 4
21 11 32 23 12 52 13 51 21 2 0 0 0 0 2 0 2 8
21 11 21 12 42 33 23 11 41 2 0 0 1 0 1 1 1 8
21 11 32 21 12 52 13 51 23 2 0 0 1 0 2 2 2 8
21 11 22 13 21 13 21 12 41 2 0 0 1 1 2 2 1 8
21 11 22 11 51 41 11 52 21 2 0 0 1 2 0 0 1 4
21 11 22 12 51 31 52 21 51 2 0 0 1 2 0 1 0 8
21 11 22 42 51 21 51 13 41 2 0 0 1 2 2 1 1 8
21 11 22 11 52 11 23 11 41 2 0 0 2 0 1 1 0 2
21 11 22 51 12 41 13 52 23 2 0 0 2 1 0 0 1 2
21 11 23 11 33 51 21 12 41 2 0 0 2 2 0 0 0 8
21 11 21 12 23 42 11 43 51 2 0 1 0 1 1 1 0 8
21 11 22 32 42 13 22 11 43 2 0 1 0 1 1 2 2 8
21 11 23 31 23 41 13 22 11 2 0 1 1 0 2 2 1 8
21 11 21 41 51 33 21 52 31 2 0 1 1 1 0 1 0 8
21 11 21 41 51 21 13 22 11 2 0 1 1 1 0 2 2 4
21 11 21 12 21 41 11 22 11 2 0 1 1 1 1 2 1 8
21 11 22 51 21 51 42 13 43 2 0 1 1 2 0 1 2 8
21 11 23 31 41 33 23 52 31 2 0 1 1 2 0 2 1 8
11 21 12 22 12 31 21 13 41 2 0 1 1 2 2 0 1 4
21 11 21 12 22 33 21 11 41 2 0 1 2 0 0 1 0 8
21 11 22 12 23 51 31 52 21 2 0 1 2 0 0 2 2 8
21 11 21 11 23 13 42 13 43 2 0 1 2 0 1 0 0 8
21 11 21 51 11 51 23 12 43 2 0 1 2 0 1 1 2 4
21 11 21 42 13 43 13 23 11 2 0 1 2 0 2 2 0 8
21 11 21 32 42 31 23 13 41 2 0 1 2 1 2 1 0 8
21 11 21 42 31 23 13 43 51 2 0 1 2 2 0 1 1 8
21 11 22 11 21 42 13 32 43 2 0 1 2 2 0 2 0 8
21 11 21 43 11 23 43 11 43 2 0 1 2 2 1 0 1 8
21 11 22 33 22 42 13 43 51 2 0 1 2 2 1 1 0 4
21 12 21 43 52 21 12 32 41 2 0 2 0 0 1 0 1 2
21 11 22 42 11 52 33 51 21 2 0 2 0 1 0 1 0 2
21 11 21 12 22 13 21 12 43 2 0 2 1 0 1 1 2 8
21 11 21 12 22 13 21 12 41 2 0 2 1 0 2 1 1 8
21 11 21 12 21 43 11 22 11 2 0 2 1 1 1 1 1 8
21 11 23 33 42 51 21 13 41 2 0 2 1 2 1 0 1 4
21 11 21 12 21 32 22 11 41 2 0 2 2 0 0 1 2 8
21 11 21 12 21 32 22 11 43 2 0 2 2 0 2 1 0 8
21 11 22 11 51 41 11 52 23 2 1 0 0 0 0 2 1 4
21 11 32 21 12 52 13 51 21 2 1 0 0 2 2 0 2 8
21 11 21 12 31 23 11 41 51 2 1 0 1 1 0 1 0 8
21 11 51 23 51 43 13 22 13 2 1 0 1 2 0 2 1 4
21 11 22 31 52 23 52 13 43 2 1 0 1 2 1 0 2 8
21 11 21 11 31 23 12 41 12 2 1 0 2 0 0 0 1 8
21 11 21 32 21 13 22 11 41 2 1 0 2 1 1 2 0 8
21 11 22 51 43 11 21 42 11 2 1 1 0 0 2 1 2 8
21 11 31 21 13 42 33 43 12 2 1 1 0 0 2 2 1 4
21 11 31 21 13 42 33 41 12 2 1 1 0 1 2 2 0 4
21 11 22 32 41 13 22 11 22 2 1 1 0 2 0 1 2 4
21 11 21 11 22 11 21 11 41 2 1 1 1 0 0 0 1 8
21 11 21 32 21 41 13 22 11 2 1 1 1 1 1 2 0 8
11 22 31 21 12 31 21 11 41 2 1 1 1 2 1 2 2 4
21 11 21 11 51 21 11 41 13 2 1 1 2 0 2 0 1 8
21 11 22 12 23 11 22 11 41 2 1 1 2 1 2 2 1 2
21 11 22 42 52 23 52 13 43 2 1 1 2 2 1 0 0 8
21 11 21 42 32 23 13 22 43 2 1 2 0 1 0 1 2 4
21 11 21 42 32 23 13 22 41 2 1 2 0 1 2 1 0 4
21 11 31 21 11 31 51 52 21 2 1 2 1 0 0 0 0 4
21 11 21 13 33 43 13 23 11 2 1 2 1 0 1 2 0 8
21 11 21 13 21 41 11 21 11 2 1 2 1 0 2 0 1 8
21 11 21 13 33 43 11 23 11 2 1 2 1 1 1 1 0 8
21 11 21 13 21 43 11 21 11 2 1 2 1 1 2 0 0 8
21 11 22 51 21 51 13 43 12 2 1 2 1 1 2 1 2 2
21 11 21 51 12 32 41 13 23 2 1 2 1 1 2 2 1 8
21 11 21 11 43 13 51 11 23 2 1 2 2 1 1 1 2 4
21 11 22 51 12 41 13 52 21 2 2 0 0 0 0 1 1 2
21 11 21 12 23 11 22 41 12 2 2 0 0 0 1 0 1 8
21 11 22 32 23 33 23 13 43 2 2 0 1 0 1 1 2 8
21 11 21 33 21 32 22 13 43 2 2 0 1 0 2 1 1 4
21 11 21 13 22 41 31 23 33 2 2 0 2 1 0 1 1 4
21 11 21 11 33 52 23 12 41 2 2 0 2 2 0 1 0 8
21 11 21 32 21 32 22 13 43 2 2 0 2 2 2 1 1 8
21 11 21 51 13 21 51 41 12 2 2 1 0 0 2 1 1 4
21 11 22 32 51 21 51 13 41 2 2 1 0 2 2 1 2 8
21 11 22 13 43 51 41 33 41 2 2 1 0 2 2 2 1 8
21 11 51 21 12 22 51 33 41 2 2 1 1 0 0 0 0 4
21 11 21 12 21 51 33 51 41 2 2 1 1 0 2 0 1 8
21 11 21 12 21 11 22 13 41 2 2 1 1 1 1 0 1 8
21 11 21 33 41 33 21 52 33 2 2 1 1 1 2 1 2 8
21 11 21 12 51 33 23 51 41 2 2 1 2 0 0 1 1 8
21 11 21 11 22 31 21 12 43 2 2 1 2 0 1 1 0 8
21 11 21 32 21 33 22 13 43 2 2 1 2 0 2 1 2 8
21 11 21 11 51 11 41 13 23 2 2 1 2 0 2 2 1 8
21 11 21 32 22 33 21 13 43 2 2 1 2 2 0 1 2 8
21 11 21 11 51 11 41 13 21 2 2 1 2 2 2 0 1 8
21 11 21 13 43 13 23 13 51 2 2 2 0 0 0 2 1 8
21 11 21 13 22 41 31 23 31 2 2 2 0 1 0 1 1 4
21 11 21 13 22 43 31 23 31 2 2 2 0 1 1 0 1 4
21 11 21 13 43 11 23 11 22 2 2 2 0 1 1 1 0 4
21 11 21 13 21 43 13 21 11 2 2 2 1 0 2 0 0 8
21 11 21 33 21 33 22 13 41 2 2 2 1 0 2 1 2 8
21 11 21 11 43 13 51 11 21 2 2 2 1 1 1 1 2 4
21 11 21 13 21 43 13 21 13 2 2 2 1 2 0 0 0 8
21 11 21 11 22 13 21 13 43 2 2 2 1 2 1 0 2 8
21 11 21 11 22 13 21 13 41 2 2 2 1 2 2 0 1 8
21 11 21 11 21 12 22 12 41 2 2 2 2 0 0 0 1 8
21 11 21 13 23 31 21 33 41 2 2 2 2 0 0 2 2 4
21 11 21 11 22 33 21 12 43 2 2 2 2 0 1 1 2 8
21 11 21 11 22 33 21 12 41 2 2 2 2 0 2 1 1 8
21 11 21 13 23 31 21 33 43 2 2 2 2 0 2 2 0 4
21 11 21 31 42 33 23 13 41 2 2 2 2 1 1 1 1 1
21 11 22 32 51 11 52 33 21 2 2 2 2 2 0 2 0 4
21 11 21 31 21 33 22 13 41 2 2 2 2 2 2 1 2 8
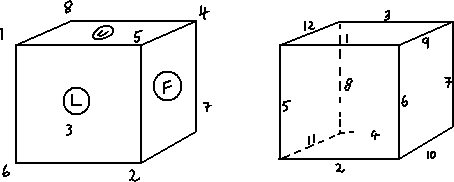
STAGE 3: GETTING INTO THE SQUARES GROUP
Corners and edges are numbered as in the above diagrams.
Moves are coded as follows:
1=L, 2=L
2, 3=L', 4=F
2, 5=R, 6=R
2, 7=R', 8=B
2, 9=U
2, 10=D
2.
To accomplish stage 3, proceed as follows:
(i) Establish which corners are out of orbit.
(ii) Perform moves as indicated in the table below.
(iii) Find by calculation the right coset of the squares group
in which the permutation of corners now lies.
(iv) Refer to the appropriate detailed table. Find the numbers
of the positions of the four edge pieces of the FB-slice,
i.e. LU, LD, RU, RD. Find the number in the left-hand
column corresponding to these, and perform the inverse of
the given move. since some cosets are reflections of
others, the reader may have to undertake the extra task
of reflecting his position to find a suitable table.
CORNERS OUT OF ORBIT | INITIAL MOVE
1,5 | -
1,6 | -
1,7 | 4
1,8 | 2 9
1,2,5,6 | 1
1,2,5,7 | 1 4
1,2,5,8 | 3 9
1,2,7,8 | -
1,3,6,8 | 9
1,3,5,7 | 6 4
1,3,5,8 | 1 9
1,2,3.5,6,7 | 1
1,2,3,5,7,8 | 4 5
1,2,3,6,7,8 | 1 5 9
1,2,3,4,5,6,7,8 | 1 5
page 1
CORNERS OUT OF ORBIT: NONE COSET: G COSET: G(14)(68)
1234 - 1 4 1 4 1 5 8 1 8 7
1235 1 4 1 7 4 10 2 7 1 4 1 4 9 2 9 7 4 7
1236 1 4 1 7 4 10 7 8 1 4 1 4 2 9 1 8 10 7
1237 1 4 1 7 4 10 7 4 1 4 1 4 2 8 9 7 9 7
1238 1 4 1 7 4 9 3 10 1 4 3 4 2 8 10 1 8 3
1245 1 4 1 7 4 10 2 5 1 4 1 4 2 9 1 4 10 7
1246 1 4 1 7 4 10 5 8 1 4 1 4 9 2 9 3 9 3
1247 1 4 1 7 4 10 5 4 1 4 3 4 1 5 8 3 8 10 3
1248 1 4 1 7 4 9 1 9 1 4 1 4 2 8 9 3 8 3
1256 1 4 1 7 4 8 10 5 1 4 1 4 1 5 8 1 4 3
1257 1 4 1 4 8 3 10 7 1 4 1 4 2 9 1 10 5 4
1258 1 4 1 4 8 3 10 5 1 4 3 4 1 5 9 8 1 4 3
1267 1 4 1 4 8 7 8 1 1 4 3 4 2 4 9 1 10 7
1268 1 4 5 9 10 3 4 3 1 4 1 4 2 4 10 3 9 7
1278 1 4 1 7 9 1 9 10 1 4 1 4 2 10 1 8 5 10
1345 1 4 1 7 4 9 3 8 1 4 1 4 10 2 10 7 10 7
1346 1 4 1 4 8 3 9 1 1 4 1 4 1 5 4 5 8 3
1347 1 4 1 7 4 9 3 6 1 4 1 4 2 10 1 4 1 4
1348 1 4 1 7 4 9 2 1 1 4 1 4 2 9 1 8 9 3
1356 1 4 1 9 10 3 9 5 1 4 3 4 2 9 7 4 10 7
1357 1 4 8 1 4 3 7 8 1 4 3 4 2 9 7 9 1 8
1358 1 4 2 9 4 6 10 3 1 4 1 4 2 4 9 7 10 7
1367 1 4 2 9 4 6 9 7 1 4 3 4 2 4 10 1 8 7
1368 1 4 8 1 4 3 7 4 1 4 3 4 2 8 9 1 9 7
1378 1 4 1 7 9 1 9 6 1 4 3 4 2 9 7 9 1 9
1456 1 4 1 9 10 3 9 7 1 4 3 4 2 10 3 9 5 10
1457 1 4 1 7 9 1 8 9 1 4 1 4 2 10 1 8 5 8
1458 1 4 8 1 9 3 7 9 1 4 1 4 2 8 10 3 9 3
1467 1 4 8 1 9 1 5 9 1 4 1 4 1 4 3 10 3 9 7
1468 1 4 1 7 9 1 4 9 1 4 1 4 2 10 1 8 5 4
1478 1 4 1 7 9 1 6 9 1 4 1 4 10 6 9 3 4 7
1567 1 4 8 2 9 8 10 1 1 4 1 4 9 6 10 3 9 7
1568 1 4 8 2 9 4 10 3 1 4 1 4 1 9 3 10 3 8 3
1578 1 4 8 9 4 10 3 4 3 8 3 8 9 6 10 1 9 5 4
1578 1 4 8 9 4 9 7 9 3 8 3 8 3 9 1 10 1 4 1 8
2345 1 4 1 4 8 3 9 3 1 4 1 4 1 5 4 1 9 7
2346 1 4 1 7 4 10 5 9 1 4 1 4 10 2 10 3 4 3
2347 1 4 1 7 4 9 1 6 1 4 1 4 2 9 1 4 9 3
2348 1 4 1 7 4 9 1 4 1 4 1 4 2 10 5 9 5 8
2356 1 4 3 9 10 1 10 5 1 4 1 4 2 9 1 10 5 9
2357 1 4 1 7 9 1 8 10 1 4 1 4 6 9 1 4 5 8
2358 1 4 8 1 9 3 7 10 1 4 1 4 1 4 7 8 7 10 7
2367 1 4 8 1 9 1 5 10 1 4 1 4 2 8 10 3 10 7
2368 1 4 1 7 9 1 4 10 1 4 1 4 2 4 9 3 8 7
2378 1 4 1 7 9 1 6 10 1 4 1 4 10 2 10 3 8 7
2456 1 4 1 9 10 7 4 1 1 4 3 4 2 9 3 9 4 3
2457 1 4 8 1 1 1 5 8 1 4 3 4 2 8 9 5 8 3
2458 1 4 2 9 4 2 10 7 1 4 3 4 6 8 9 1 4 7
2467 1 4 2 9 4 2 9 3 1 4 1 4 2 4 9 3 4 3
2468 1 4 8 1 4 1 5 4 1 4 3 4 6 10 7 10 1 4
2478 1 4 1 7 9 1 9 2 1 4 1 4 1 5 4 1 10 3
2567 1 4 8 2 9 8 10 3 1 4 1 4 1 9 3 10 7 9 7
2568 1 4 8 2 9 4 10 1 1 4 1 4 9 2 9 3 10 7
2578 1 4 8 9 4 10 1 4 3 8 3 8 3 9 1 10 5 9 5 4
2678 1 4 8 9 4 9 5 10 3 8 3 8 9 2 9 1 10 5 8
3456 1 4 1 7 9 1 4 8 1 4 1 4 1 9 3 9 3 9 3
3457 1 4 1 7 9 1 6 8 1 4 3 4 6 4 9 5 10 3
3458 1 4 1 7 9 1 4 2 1 4 1 4 2 8 9 3 4 7
3467 1 4 1 7 9 1 4 6 1 4 1 4 6 4 10 3 8 7
3468 1 4 1 7 9 1 6 4 1 4 3 4 2 8 10 5 9 3
3478 1 4 1 5 9 2 10 1 1 4 1 4 2 10 1 8 5 9
3567 1 4 8 9 4 9 7 8 7 8 7 8 10 6 10 5 9 1 8
3568 1 4 8 9 4 10 3 9 7 8 7 8 7 10 5 9 1 10 1 4
3578 1 4 8 2 9 8 9 5 5 4 5 4 10 6 10 7 9 3
3678 1 4 8 2 9 4 9 7 5 6 5 4 5 10 7 9 3 10 3
4567 1 4 8 9 4 9 5 8 7 8 7 8 7 10 5 9 5 4 5 8
4568 1 4 8 9 4 10 1 10 7 8 7 8 10 2 9 5 10 1 4
4578 1 4 8 2 9 8 9 7 5 4 5 4 5 10 7 9 7 8 7
4678 1 4 8 2 9 4 9 5 5 4 5 4 10 2 9 7 10 3
5678 1 4 1 7 9 4 8 5 1 10 9 8 1 4 2 9 1 9 1
Page 2
ALL CORNERS IN ORBIT. COSET: G(12) COSET: G(14)
1234 1 4 2 9 1 4 2 4 9 1 1 4 2 9 1 4 2 4 9 1 4
1235 1 4 2 9 1 4 2 10 5 1 4 2 9 3 4 2 9 1 6 4
1236 1 4 2 9 1 4 6 9 7 1 4 2 9 3 4 1 5 8 5 8
1237 1 4 2 9 3 4 6 10 1 4 8 1 4 2 9 3 4 1 5 8 5 4
1238 1 4 2 9 3 4 6 10 3 4 8 1 4 2 9 3 4 2 9 1 6 8
1245 1 4 2 9 1 4 2 10 7 1 4 2 9 3 4 2 9 1 4 10
1246 1 4 2 9 1 4 6 9 5 1 4 2 9 3 4 1 5 8 7 8
1247 1 4 2 9 3 4 2 9 3 4 8 1 4 2 9 3 4 1 5 8 7 4
1248 1 4 2 9 3 4 2 9 1 4 8 1 4 2 9 1 4 2 9 1 10 6
1256 1 4 2 9 1 4 2 4 10 5 1 4 2 9 7 4 2 4 9 3 8 10
1257 1 4 2 9 3 9 1 4 8 5 8 3 1 4 2 9 1 4 2 4 10 5 4
1258 1 4 2 9 3 9 1 9 10 5 8 5 1 4 2 9 7 4 2 4 9 3 10 2
1267 1 4 2 9 3 9 1 4 8 1 9 5 1 4 2 9 7 4 2 4 9 3 10 6
1268 1 4 2 9 3 9 1 4 8 1 9 7 1 4 2 9 1 4 2 4 10 5 8
1278 1 4 2 9 1 4 2 4 10 5 4 8 1 4 2 9 7 4 2 4 9 3 4 10
1345 1 4 2 9 3 4 6 10 3 9 10 1 4 2 9 3 4 2 9 3 9 2
1346 1 4 2 9 3 4 6 10 1 9 10 1 4 2 9 3 4 2 9 1 9 2
1347 1 4 2 9 3 4 6 4 8 9 7 1 4 2 9 3 4 6 10 1 4 10
1348 1 4 2 9 3 4 6 4 8 9 5 1 4 2 9 3 4 6 10 3 8 10
1356 7 4 6 9 5 4 7 4 8 3 10 3 1 4 2 9 1 9 2 10 4 1 9 2
1357 1 4 2 9 3 4 9 6 4 9 5 7 4 6 9 5 4 7 4 8 3 10 3 4
1358 1 4 2 9 3 6 2 4 9 1 6 1 4 2 9 3 4 6 4 9 5 4
1367 1 4 2 9 3 4 1 5 9 4 3 1 4 2 9 3 4 6 4 10 1 4
1368 1 4 2 9 3 4 9 6 8 9 7 5 8 6 9 7 8 5 8 4 1 10 1 8
1378 1 4 2 9 3 4 1 4 8 5 10 5 1 4 2 9 1 9 2 9 8 5 9 6
1456 7 4 6 9 5 4 7 9 10 7 8 1 1 4 2 9 3 4 2 4 9 1 4
1457 1 4 2 9 3 4 1 5 10 4 3 1 4 2 9 1 4 2 1 10 5 4 10
1458 1 4 2 9 3 4 9 2 8 9 3 1 4 2 9 7 4 9 2 4 9 3 4
1467 1 4 2 9 3 4 9 2 4 9 1 1 4 2 9 7 4 9 2 8 9 1 4
1468 1 4 2 9 3 4 1 5 10 8 7 1 4 2 9 7 4 2 4 9 1 9 2
1478 1 4 2 9 3 4 1 4 8 1 8 3 1 4 2 9 3 4 2 4 9 1 8
1567 1 4 2 9 3 4 1 5 4 2 1 1 4 2 9 3 4 1 5 4 3 4
1568 1 4 2 9 3 4 1 5 4 3 6 1 4 2 9 3 4 2 10 2 7 8
1578 1 4 2 9 3 4 6 9 5 4 8 1 4 2 9 3 4 2 10 2 7 4
1678 1 4 2 9 3 4 6 9 7 4 8 1 4 2 9 3 4 1 5 4 3 8
2345 1 4 2 9 3 4 2 9 1 9 10 1 4 2 9 3 4 2 9 1 4 9
2346 1 4 2 9 3 4 2 9 3 9 10 1 4 2 9 3 4 2 9 3 8 9
2347 1 4 2 9 3 4 2 4 8 10 5 1 4 2 9 3 4 2 9 3 4 9
2348 1 4 2 9 3 4 2 4 8 10 7 1 4 2 9 3 4 2 9 1 8 9
2356 5 4 6 10 7 4 5 10 9 5 8 3 1 4 2 9 3 4 2 4 10 5 4
2357 1 4 2 9 3 4 1 5 9 4 1 1 4 2 9 1 4 2 4 10 5 4 9
2358 1 4 2 9 3 4 9 2 4 10 5 1 4 2 9 7 4 9 2 8 10 5 4
2367 1 4 2 9 3 4 9 2 8 10 7 1 4 1 9 7 4 9 2 4 10 7 4
2368 1 4 2 9 3 4 1 5 9 8 5 1 4 2 9 1 9 2 9 8 5 4 10
2378 1 4 2 9 3 4 1 9 10 1 8 7 1 4 2 9 3 4 2 4 10 5 8
2456 5 4 6 10 7 4 5 4 8 1 9 1 1 4 2 9 1 9 2 10 4 1 9 6
2457 1 4 2 9 3 4 9 2 4 9 3 5 4 6 10 7 4 5 4 8 1 9 1 4
2458 1 4 2 9 3 4 2 8 9 2 3 1 4 2 9 3 4 2 4 10 7 4
2467 1 4 2 9 3 1 1 5 9 8 7 1 4 2 9 3 4 2 4 9 3 4
2458 1 4 2 9 3 4 9 2 8 9 1 7 8 6 10 5 8 7 8 4 3 9 3 8
2478 1 4 2 9 3 4 1 4 8 1 8 1 1 4 2 9 1 4 2 8 9 1 9 2
2567 1 4 2 9 3 4 1 5 4 2 3 1 4 2 9 3 4 1 5 4 1 4
2568 1 4 2 9 3 4 1 5 4 1 6 1 4 2 9 3 4 2 10 5 9 6
2578 1 4 2 9 3 4 2 10 7 4 8 1 4 2 9 3 4 2 10 7 4 9
2678 1 4 2 9 3 4 2 10 5 4 8 1 4 2 9 3 4 1 5 4 1 8
3456 1 4 2 9 1 4 2 4 10 5 9 10 1 4 2 9 7 4 2 4 9 3 8 9
3457 7 4 6 9 5 9 7 4 8 7 9 1 1 4 2 9 1 4 1 5 10 8 5 8
3458 5 8 6 9 7 9 5 8 4 5 9 1 7 4 6 9 1 4 6 4 9 5 10 6
3467 7 4 6 9 5 9 7 4 8 7 9 3 5 8 6 9 3 8 6 8 9 7 10 6
3468 5 8 6 9 7 9 5 8 4 5 9 3 1 4 2 9 1 4 1 5 10 8 5 4
3478 1 4 2 9 3 6 4 2 4 10 5 1 4 2 9 7 4 2 4 9 3 4 9
3567 1 4 2 9 3 4 6 9 7 9 10 1 4 2 9 3 4 2 10 7 10 6
3568 1 4 2 9 3 4 6 9 5 9 10 1 4 2 9 3 4 2 10 5 10 6
3578 1 4 2 9 3 4 6 4 8 10 3 1 4 2 9 3 4 6 9 5 4 9
3678 1 4 2 9 3 4 6 4 8 10 1 1 4 2 9 3 4 6 9 7 8 9
4567 1 4 2 9 3 4 2 10 5 9 10 1 4 2 9 3 4 2 10 5 4 10
4568 1 4 2 9 3 4 2 10 7 9 10 1 4 2 9 3 4 2 10 7 8 10
4578 1 4 2 9 3 4 2 4 8 9 1 1 4 2 9 3 4 2 10 7 4 10
4678 1 4 2 9 3 4 2 4 8 9 3 1 4 2 9 3 4 2 10 5 8 10
5678 1 4 2 9 3 6 4 2 4 9 1 1 4 2 9 1 8 2 4 9 5 4
Page 3
CORNERS:(18)(27) COSET:G COSET: G(14)(68)
1234 1 4 1 4 9 4 3 4 1 1 4 3 8 10 2 9 3 4 1
1235 1 4 1 4 10 8 3 9 3 3 9 3 9 3 9 5 10 3 4 3
1236 1 4 1 4 10 8 3 9 1 3 9 3 9 3 9 5 10 3 4 1
1237 1 4 1 4 8 1 9 4 5 1 4 3 8 2 8 10 3 4 1
1238 1 4 1 6 9 10 3 8 1 1 4 3 9 2 8 5 9 8 5
1245 1 4 2 9 2 9 4 9 1 3 9 3 9 3 9 1 8 7 8 1
1246 1 4 1 4 10 8 7 4 7 3 9 3 9 3 9 1 8 7 8 3
1247 1 4 1 6 9 10 7 9 7 1 4 3 9 2 8 1 4 9 1
1248 1 4 1 4 8 1 9 4 7 1 4 3 8 2 8 10 7 10 7
1256 1 4 9 3 4 8 3 10 8 1 1 4 3 4 2 4 10 3 9 5
1257 1 4 1 4 9 8 3 10 7 1 4 3 4 9 6 10 3 10 7
1258 1 4 1 4 9 8 3 10 5 1 4 3 4 9 2 9 7 4 1
1267 1 4 1 4 9 8 7 8 1 1 4 3 4 9 2 9 3 9 5
1268 1 4 1 10 8 9 7 4 7 1 4 3 4 9 2 9 3 9 7
1278 7 10 7 9 4 9 5 9 7 9 10 1 4 9 1 9 2 4 3 9 5
1345 1 4 1 6 4 8 3 4 1 1 4 3 4 2 4 9 3 4 1
1346 1 4 1 8 9 4 3 9 1 1 4 3 10 2 9 4 3 4 1
1347 1 4 1 5 4 9 4 10 7 1 4 3 4 2 8 9 7 9 7
1348 1 4 1 5 4 9 4 10 5 1 4 3 4 2 8 9 3 8 1
1356 1 4 1 4 9 8 3 10 1 1 4 3 6 9 2 4 7 8 1
1357 1 4 1 7 4 2 4 1 6 1 4 3 8 2 8 9 3 9 5
1358 1 4 1 5 4 2 1 4 8 1 4 3 4 1 5 4 1 10 7
1367 1 4 1 5 4 1 4 8 2 1 4 3 4 2 10 1 9 8 7
1368 1 4 1 7 4 2 4 2 7 1 4 3 4 10 2 10 3 8 3
1378 1 4 1 4 8 1 4 2 5 1 4 3 9 2 8 5 10 8 5
1456 1 4 1 4 9 8 7 8 7 1 4 3 6 9 6 8 3 9 7
1457 1 4 1 5 4 2 7 9 10 1 4 3 4 1 5 4 1 10 5
1458 1 4 1 7 4 2 4 2 3 1 4 3 8 2 8 9 3 9 7
1467 1 4 1 7 4 1 5 9 3 1 4 3 4 10 6 9 3 4 1
1468 1 4 1 5 4 2 3 9 10 1 4 3 4 2 10 1 9 8 5
1478 1 4 1 4 8 1 4 2 7 1 4 3 9 2 8 1 8 9 3
1567 1 4 1 4 10 8 3 9 7 1 4 9 1 10 6 8 3 4 1
1568 1 4 1 4 10 8 3 9 5 1 4 9 1 10 2 4 3 8 3
1578 1 4 1 8 9 4 3 9 5 1 4 3 8 2 10 1 8 9 3
1678 1 4 1 6 4 8 7 10 1 1 4 1 4 10 2 10 1 9 5
2345 1 4 1 8 9 4 3 9 3 1 4 3 10 2 9 4 3 4 3
2346 1 4 1 6 4 8 3 4 3 1 4 3 4 2 4 9 3 4 3
2347 1 4 2 4 9 4 9 4 1 1 4 3 4 6 4 10 3 4 1
2348 1 4 2 9 2 9 8 9 7 1 4 3 4 2 8 9 3 8 3
2356 1 4 1 4 9 8 3 10 3 1 4 3 6 9 2 4 3 10 7
2357 1 4 1 5 4 2 3 4 8 1 4 3 4 6 9 1 9 4 5
2358 1 4 1 7 4 2 9 4 7 1 4 3 4 10 2 10 3 8 1
2367 1 4 1 7 4 1 5 9 5 1 4 3 8 6 4 10 3 10 7
2368 1 4 1 5 4 2 4 8 3 1 4 3 4 2 10 1 8 2 3
2378 1 4 1 4 8 1 10 4 5 1 4 3 9 6 4 1 4 10 3
2456 1 4 1 10 8 9 7 4 1 1 4 3 6 9 2 4 3 10 5
2457 1 4 1 7 4 1 5 9 1 1 4 3 4 10 2 10 7 9 7
2458 1 4 1 5 4 1 4 8 6 1 4 3 4 2 10 5 4 10 3
2467 1 4 1 5 4 1 6 4 8 1 4 3 4 1 5 4 5 4 3
2458 1 4 1 7 4 1 5 9 7 1 4 3 8 2 8 9 7 4 1
2478 1 4 1 4 8 1 10 4 7 1 4 3 9 2 8 1 8 9 1
2567 1 4 1 4 10 8 7 4 1 1 4 9 1 10 2 4 7 9 7
2568 1 4 2 9 2 9 4 9 7 1 4 9 1 10 2 4 3 8 1
2578 1 4 1 6 4 8 3 4 5 1 4 3 4 1 5 8 1 8 3
2678 1 4 1 8 9 4 7 4 1 1 4 3 8 2 10 1 8 9 1
3456 1 10 1 9 4 9 3 9 1 9 10 1 4 9 1 10 2 8 3 9 5
3457 1 4 1 4 8 1 4 2 3 1 4 3 4 2 9 1 4 9 3
3458 1 4 1 4 8 1 4 1 6 1 4 3 4 2 9 5 9 8 5
3467 1 4 1 4 8 1 4 2 1 1 4 3 4 2 9 1 4 9 1
3468 1 4 1 4 8 1 4 3 6 1 4 3 4 6 10 1 8 10 3
3478 1 4 1 8 9 8 3 8 1 1 4 5 8 10 2 10 1 10 5
3567 1 4 1 6 9 10 3 8 7 1 4 3 4 2 8 10 3 10 7
3568 1 4 1 4 8 5 8 9 5 1 4 3 10 2 4 5 9 8 5
3578 1 4 1 5 4 9 4 10 3 3 9 3 9 4 6 8 3 4 10 1
3678 1 4 1 5 4 9 4 10 1 3 9 3 9 4 6 8 3 4 10 3
4567 1 4 1 4 8 1 9 4 1 1 4 3 10 2 4 1 4 9 1
4568 1 4 1 6 9 10 3 8 5 1 4 3 4 2 8 10 3 10 5
4578 1 4 2 9 2 9 8 9 1 3 9 3 9 4 2 4 3 8 9 3
4678 1 4 2 4 9 4 9 4 7 3 9 3 9 4 2 4 3 8 9 1
5678 1 4 1 4 9 4 3 4 5 1 4 5 4 2 8 9 1 4 1
CORNERS:(18)(27) COSET:G(12) COSET: G(14)
Page 4
1234 1 4 1 4 1 4 1 4 3 9 1 4 9 1 9 2 4 3 9
1235 1 4 1 4 9 8 2 1 10 1 4 1 4 2 10 1 6 10
1236 1 4 1 4 9 8 3 10 2 1 4 1 4 2 10 3 9 6
1237 1 4 1 6 9 10 7 8 9 1 4 1 8 6 10 7 9 8
1238 1 4 1 4 8 1 9 4 6 1 4 3 8 6 4 9 7 9
1245 1 4 1 4 9 8 3 10 6 1 4 1 4 2 10 3 9 2
1246 1 4 1 4 8 1 8 9 10 1 4 1 4 1 5 4 7 9
1247 1 4 1 4 8 1 9 4 2 1 4 3 8 2 8 10 7 10
1248 1 4 1 6 8 10 8 5 10 1 4 1 8 2 9 7 10 4
1256 1 4 1 4 8 9 10 3 10 1 4 3 4 2 4 10 3 9
1257 1 4 1 4 9 4 7 8 10 1 4 1 4 9 2 9 1 10 4
1258 1 4 1 4 10 8 2 5 8 1 4 1 4 9 6 10 1 9 8 2
1267 1 4 1 5 4 6 4 10 8 1 4 1 4 9 2 9 1 10 4 2
1268 1 4 1 4 9 4 7 4 10 1 4 1 4 9 6 10 1 9 8
1278 1 4 1 4 8 9 10 5 4 1 4 3 8 10 2 9 7 10
1345 1 4 1 8 9 4 2 1 9 1 4 1 9 4 2 4 1 9
1346 1 4 1 6 4 8 1 6 8 1 4 1 4 10 2 10 1 9
1347 1 4 1 4 8 1 10 4 2 1 4 1 8 2 8 9 5 10
1348 1 4 1 4 2 6 4 1 8 1 4 1 10 2 9 8 5 10
1356 1 4 1 4 10 8 2 1 9 1 4 9 1 8 6 9 3 10
1357 1 4 1 4 3 1 4 5 8 1 4 1 4 2 9 7 10 6
1358 1 4 1 5 9 2 4 2 8 1 4 9 1 4 6 9 3 10
1367 1 4 1 5 9 2 8 2 8 1 4 9 1 4 6 10 7 9
1368 1 4 1 4 10 8 3 8 9 1 4 1 4 6 10 3 9 8
1378 1 4 1 5 9 4 9 4 10 1 4 1 4 6 4 9 5 10
1456 1 4 1 4 9 4 3 9 4 1 4 9 1 10 6 8 7 10
1457 1 4 1 7 4 1 5 9 2 1 4 1 8 2 8 10 1 9
1458 1 4 1 5 4 1 9 10 3 1 4 1 4 3 7 4 3 10
1467 1 4 1 4 1 7 10 5 9 1 4 1 8 2 10 3 9 4
1468 1 4 1 4 9 10 8 5 10 1 4 1 4 9 6 10 5 10
1478 1 4 1 5 4 9 4 10 6 1 4 1 8 2 10 7 10 2
1567 1 4 1 4 8 5 10 4 8 1 4 1 4 6 4 10 1 9
1568 1 4 1 4 9 8 7 8 6 1 4 1 10 2 8 3 9 6
1578 1 4 1 6 4 8 7 8 10 1 4 1 9 6 8 7 10 8
1678 1 4 1 4 10 4 3 9 8 1 4 3 10 2 9 4 7 10
2345 1 4 1 6 4 8 2 1 4 1 4 1 4 10 6 9 1 10
2346 1 4 1 4 10 4 7 4 9 1 4 1 9 4 6 8 1 10
2347 1 4 1 4 1 7 9 5 4 1 4 1 10 6 10 4 5 9
2348 1 4 1 4 8 1 10 4 6 1 4 1 8 2 9 7 9 4
2356 1 4 1 4 9 4 3 10 4 1 4 9 1 10 2 4 7 9
2357 1 4 1 7 4 2 9 4 6 1 4 1 4 9 2 9 5 9
2358 1 4 1 4 2 6 8 1 10 1 4 1 8 6 9 3 10 8
2367 1 4 1 4 10 6 7 9 4 1 4 1 1 1 5 8 3 9
2368 1 4 1 4 9 10 8 1 8 1 4 1 8 6 4 9 1 10
2378 1 4 1 5 4 9 4 10 2 1 4 1 8 2 10 7 10 6
2456 1 4 1 4 10 8 1 6 10 1 4 9 1 8 2 10 3 9
2457 1 4 1 5 4 1 4 8 7 1 4 1 4 2 9 3 9 4
2458 1 4 1 5 9 2 8 6 4 1 4 9 1 4 2 9 7 10
2467 1 4 1 5 9 2 4 6 4 1 4 9 1 4 2 10 3 9
2458 1 4 1 4 1 7 10 1 4 1 4 1 4 2 9 7 10 2
2478 1 4 1 1 7 4 9 4 9 1 4 1 4 2 8 10 5 9
2567 1 4 1 4 9 8 7 8 2 1 4 1 10 2 8 3 9 2
2568 1 4 1 4 9 8 2 5 4 1 4 1 4 2 8 9 1 10
2578 1 4 1 8 9 4 2 5 8 1 4 3 10 6 10 8 7 9
2678 1 4 1 6 4 8 2 5 9 1 4 1 9 2 4 7 9 4
3456 1 4 1 4 8 9 10 1 10 1 4 1 4 2 4 9 1 9
3457 1 4 1 8 9 8 7 8 9 1 4 1 4 1 4 7 8 1 9
3458 1 4 1 5 4 2 4 10 8 1 4 1 4 1 4 3 10 5 10 2
3467 1 4 1 5 4 6 4 9 8 1 4 1 4 1 4 7 8 1 9 2
3468 1 4 1 8 9 8 7 4 9 1 4 1 4 1 4 3 10 5 10
3478 1 4 1 6 8 9 8 1 4 1 4 1 8 9 2 10 5 10
3567 1 4 1 4 8 5 4 8 9 1 4 1 4 6 9 7 9 8
3568 1 4 1 6 8 10 8 1 8 1 4 1 6 10 2 4 1 10
3578 1 4 1 4 8 1 4 1 5 1 4 1 9 6 8 7 9 8
3678 1 4 1 4 3 1 8 5 9 1 4 1 4 6 8 9 5 9
4567 1 4 1 6 9 10 1 6 4 1 4 1 6 10 6 8 1 9
4568 1 4 1 4 8 2 7 4 10 1 4 1 4 2 9 7 10 2
4578 1 4 1 4 1 7 9 1 10 1 4 1 4 2 4 10 5 10
4678 1 4 1 4 8 1 4 3 7 1 4 1 9 2 4 7 10 4
5678 1 4 1 4 1 4 1 4 7 4 1 4 9 1 10 2 8 3 9
CORNERS: (13). COSET:G(12) COSET: G(14) Page 5
1234 1 4 3 4 1 4 9 1 9 1 9 1 4 1 4 2 4 3 4 5 9 5
1235 1 4 3 6 9 7 10 1 8 10 1 1 4 1 4 1 4 2 9 10 4 2
1236 1 4 3 4 1 10 3 10 3 10 8 1 4 1 4 1 4 2 3 1 4 10
1237 1 4 3 4 5 10 4 5 4 3 10 1 4 1 4 1 4 2 8 9 10 2
1238 1 4 3 4 1 8 10 1 8 1 10 1 4 1 4 1 4 2 8 6 9 10
1245 1 4 3 6 9 3 4 5 4 9 3 1 4 1 4 1 4 2 4 9 2 9
1246 1 4 3 6 9 8 1 4 3 4 3 1 4 1 4 1 4 2 4 2 9 2
1247 1 4 3 6 9 4 5 8 3 4 3 1 4 1 4 1 4 8 9 10 2 8
1248 1 4 3 4 9 7 4 9 7 9 7 1 4 1 4 1 4 2 8 2 6 9
1256 1 4 3 4 1 4 9 2 3 10 5 1 4 1 4 1 5 4 8 2 3 4
1257 1 4 3 4 5 8 3 8 10 3 10 1 4 1 4 2 8 7 4 9 4 8
1258 1 4 3 4 8 9 1 9 7 8 1 1 4 1 4 9 2 9 6 4 5 8
1267 1 4 3 6 10 8 5 9 3 8 3 1 4 1 4 1 7 4 8 2 1 4
1268 1 4 3 4 5 8 3 4 9 5 9 1 4 1 4 2 4 7 9 1 4 1
1278 1 4 3 6 10 3 4 9 3 8 1 10 1 4 1 4 2 4 9 4 10 5 8
1345 3 8 1 6 8 1 9 8 5 4 3 1 4 1 4 1 4 1 6 8 1 8
1346 1 4 3 6 4 3 9 4 7 8 1 1 4 1 4 1 4 1 5 9 1 5
1347 1 4 3 4 1 8 10 1 8 1 6 1 4 1 4 1 4 2 6 9 6 8
1348 1 4 3 4 1 8 10 1 8 2 3 1 4 1 4 1 4 2 8 9 6 9
1356 1 4 3 4 5 9 3 4 8 10 5 1 4 1 4 1 7 8 3 10 6 8
1357 1 4 3 4 1 8 3 4 8 9 5 1 4 1 4 2 4 10 2 4 5 8
1358 1 4 3 4 1 9 1 6 10 4 5 1 4 1 4 2 8 7 4 2 4 8
1367 1 4 3 6 8 3 9 5 8 9 3 1 4 1 4 2 8 10 4 7 8 2
1368 1 4 3 6 4 3 4 5 4 10 3 1 4 1 4 1 5 9 2 4 7 8
1378 1 4 3 6 10 3 4 9 7 9 7 1 4 1 4 10 7 4 10 8 6 4
1456 1 4 3 4 1 4 3 9 10 8 3 1 4 1 4 1 7 8 3 6 8 10
1457 1 4 3 4 1 9 1 6 10 4 7 1 4 1 4 2 4 8 9 8 1 4
1458 1 4 3 4 1 8 3 4 8 9 7 1 4 1 4 1 5 10 1 4 2 4
1467 1 4 3 6 4 7 10 1 8 9 1 1 4 1 4 2 4 8 5 8 9 2
1468 1 4 3 6 8 7 4 1 4 10 1 1 4 1 4 2 4 9 10 4 1 8
1478 1 4 3 6 10 3 4 9 3 8 1 1 4 1 4 2 8 7 10 4 9 4
1567 5 8 7 8 5 4 10 5 8 3 1 4 1 4 6 4 10 4 10 5 8
1568 7 4 5 4 7 8 10 7 4 1 1 4 1 4 9 4 1 5 9 3 4
1578 1 4 3 4 1 8 10 1 4 7 9 1 4 1 4 8 10 8 2 10 5 8
1678 1 4 3 4 5 10 4 5 8 5 9 1 4 1 4 10 5 8 9 3 10 5
2345 1 4 3 4 1 4 1 4 2 8 1 1 4 1 4 1 4 6 10 8 10 4
2346 1 4 3 4 1 4 1 8 2 8 3 1 4 1 4 1 4 2 6 8 2 8
2347 1 4 3 4 2 4 1 4 1 8 1 1 4 1 4 1 4 9 4 9 6 4
2348 1 4 3 4 1 10 3 4 9 7 9 1 4 1 4 1 4 6 8 10 4 8
2356 1 4 3 4 1 4 3 4 5 4 8 1 4 1 4 2 8 7 9 4 9 8
2357 1 4 3 4 1 8 1 10 6 10 5 1 4 1 4 1 5 10 1 10 6 8
2358 1 4 3 4 1 8 2 1 9 2 7 1 4 1 4 1 5 10 1 8 6 8
2367 1 4 3 4 1 8 9 5 4 5 9 1 4 1 4 1 4 1 9 2 5 4
2368 1 4 3 4 1 8 1 9 2 9 7 1 4 1 4 1 5 10 1 9 6 4
2378 1 4 3 4 1 4 3 4 7 9 6 1 4 1 4 1 7 8 2 3 8 9
2456 1 4 3 4 1 9 8 1 10 8 5 1 4 1 4 1 9 2 1 8 1 8
2457 1 4 3 4 1 8 1 6 9 3 9 1 4 1 4 1 5 4 10 2 3 8
2458 1 4 3 4 1 8 1 10 6 10 7 1 4 1 4 1 4 6 4 1 10 5
2467 1 4 3 4 1 8 1 9 2 9 5 1 4 1 4 2 4 10 8 7 4 6
2458 1 4 3 4 10 3 4 9 7 4 1 1 4 1 4 1 8 2 8 1 10 5
2478 1 4 3 1 1 4 2 1 4 7 9 1 4 1 4 1 7 8 3 9 6 4
2567 1 4 3 4 1 4 2 10 7 4 1 1 4 1 4 1 6 8 9 1 10 5
2568 1 4 3 4 1 4 6 9 3 10 7 1 4 1 4 1 5 9 2 8 3 4
2578 3 8 1 8 2 8 3 4 3 10 7 1 4 1 4 1 9 2 3 10 7 4
2678 1 4 3 4 2 4 1 8 1 10 5 1 4 1 4 2 4 9 2 9 5 6
3456 1 4 3 4 1 9 3 4 1 9 4 1 4 1 4 1 7 10 4 2 5 4
3457 1 4 3 4 1 8 3 9 5 9 2 1 4 1 4 1 5 10 1 6 8 10
3458 1 4 3 4 1 8 1 6 10 5 10 1 4 1 4 1 5 10 2 8 7 8
3467 1 4 3 4 1 8 1 6 9 1 9 1 4 1 4 3 8 3 9 1 9 6
3468 1 4 3 4 1 8 3 10 1 10 2 1 4 1 4 1 4 2 4 5 9 5
3478 1 4 3 4 1 4 1 6 8 5 9 1 4 1 4 1 6 4 10 1 8 1
3567 1 4 3 4 9 3 10 8 3 9 7 1 4 1 4 3 8 10 1 10 7 10
3568 1 4 3 4 1 8 9 1 9 2 7 1 4 1 4 8 2 10 7 10 6 4
3578 1 4 3 4 10 3 8 5 10 3 9 1 4 1 4 9 2 9 6 8 1 4
3678 1 4 3 6 9 3 4 1 9 4 7 1 4 1 4 1 6 4 1 4 8 7
4567 1 4 3 4 1 4 3 4 9 10 3 1 4 1 4 2 4 9 2 4 1 4
4568 1 4 3 4 9 3 10 8 3 9 5 1 4 1 4 1 4 1 6 4 5 4
4578 1 4 3 6 10 3 4 1 9 3 9 1 4 1 4 2 8 9 10 3 4 9
4678 1 4 3 6 9 3 4 1 9 4 5 1 4 1 4 1 6 9 7 4 10 1
5678 1 4 3 6 4 9 1 10 3 4 1 1 4 1 4 3 8 9 5 10 3 9
page 6
CORNERS: (15). COSET: G(12) COSET: G(14)
1234 1 4 3 4 1 5 10 1 10 5 9 1 4 3 4 1 5 4 9 7 10 1
1235 1 4 3 4 1 4 1 4 6 10 4 1 4 3 4 1 4 1 8 9 8 10
1236 1 4 3 4 1 6 9 6 10 1 10 1 4 3 4 1 4 3 4 9 4 6
1237 1 4 3 4 1 10 3 9 6 4 8 1 4 3 4 2 8 1 4 9 5 10
1238 1 4 3 4 1 8 9 2 7 9 4 1 4 3 4 1 4 1 8 10 4 9
1245 1 4 3 4 1 4 1 6 10 4 6 1 4 3 4 1 4 3 8 9 8 2
1246 1 4 3 4 1 4 3 4 8 9 4 1 4 3 4 1 4 3 6 4 9 4
1247 1 4 3 4 1 4 3 4 10 8 9 1 4 3 4 3 10 7 4 1 10 1
1248 1 4 3 4 1 4 1 9 8 2 9 1 4 3 4 1 10 3 4 8 6 9
1256 1 4 3 4 1 8 10 8 9 1 10 1 4 3 4 1 8 7 4 9 8 2
1257 1 4 3 4 1 8 7 10 8 9 10 1 4 3 4 8 9 5 10 8 3 10
1258 1 4 3 4 2 8 1 10 1 9 8 1 4 3 4 2 4 5 4 3 4 8
1267 1 4 3 4 1 8 2 5 10 8 2 1 4 3 4 1 9 2 8 5 4 8
1268 1 4 3 4 1 8 3 1 7 9 4 1 4 3 4 1 8 6 10 5 9 4
1278 1 4 3 4 5 8 9 5 4 8 9 1 4 3 4 1 4 8 10 4 7 9
1345 1 4 3 4 9 2 4 7 4 7 10 1 4 3 4 1 4 1 4 8 9 8
1346 1 4 3 4 1 4 1 8 6 9 4 1 4 3 4 1 4 9 6 4 10 1
1347 1 4 3 4 1 10 3 4 8 10 2 1 4 3 4 1 4 3 10 4 10 2
1348 1 4 3 4 1 10 1 6 4 8 9 1 4 3 4 1 4 1 4 9 8 9
1356 1 4 3 4 3 8 6 10 8 3 10 1 4 3 4 1 6 8 2 10 8 1
1357 1 4 3 4 10 2 1 4 5 9 8 1 4 3 4 1 8 2 7 10 8 9
1358 1 4 3 4 9 1 8 2 8 7 10 1 4 3 4 1 8 7 10 8 9 6
1367 1 4 3 4 8 9 5 10 4 5 9 1 4 3 4 1 8 7 9 4 10 6
1368 1 4 3 4 1 8 2 9 7 9 4 1 4 3 4 1 8 1 8 1 7 4
1378 1 4 3 4 3 4 9 6 9 7 9 1 4 3 4 8 9 2 9 1 8 7
1456 1 4 3 4 1 8 7 8 9 4 10 1 4 3 4 1 8 7 4 9 8 2
1457 1 4 3 4 9 2 1 10 5 10 4 1 4 3 4 2 9 2 9 5 10 3
1458 1 4 3 4 10 3 4 5 9 8 6 1 4 3 4 1 4 9 7 8 10 4
1467 1 4 3 4 1 9 2 5 4 8 10 1 4 3 4 5 9 8 3 4 10 8
1468 1 4 3 4 9 1 6 9 5 10 8 1 4 3 4 1 7 4 8 1 10 1
1478 1 4 3 4 1 8 7 8 10 8 9 1 4 3 5 4 1 10 8 1 4 5
1567 1 4 3 4 8 9 5 8 3 10 4 1 4 3 4 8 2 10 3 9 4 1
1568 3 8 1 8 4 9 7 4 1 10 8 1 4 3 4 2 10 4 3 9 8 3
1578 1 4 3 6 4 1 9 6 8 3 9 1 4 3 4 2 8 1 4 10 1 9
1678 1 4 3 4 2 8 1 4 10 3 9 1 4 3 5 10 4 3 8 1 8 5
2345 1 4 3 4 1 10 1 9 10 6 9 1 4 3 4 1 6 8 6 10 4 1
2346 1 4 3 4 1 4 1 4 2 10 8 1 4 3 4 1 4 1 9 2 6 8
2347 1 4 3 4 1 4 1 10 8 6 9 1 4 3 4 1 4 2 4 10 7 9
2348 1 4 3 4 1 4 8 9 7 10 2 1 4 3 4 1 4 3 9 4 9 6
2356 1 4 3 4 1 4 9 2 7 9 8 1 4 3 4 1 4 2 4 10 4 1
2357 1 4 3 4 1 4 8 10 1 6 10 1 4 3 4 1 4 2 4 9 3 10
2358 1 4 3 4 1 4 6 8 10 1 10 1 4 3 4 1 4 6 4 9 7 9
2367 1 4 3 4 1 4 2 10 7 9 4 1 4 3 4 1 4 9 2 5 9 4
2368 1 4 3 4 1 4 2 8 10 5 9 1 4 3 4 1 4 9 8 9 3 10
2378 1 4 3 4 1 5 10 1 9 1 10 1 4 3 4 1 8 10 1 6 10 8
2456 1 4 3 4 1 4 9 5 9 4 6 1 4 3 4 1 4 8 9 8 2 1
2457 1 4 3 4 1 8 6 10 7 9 8 1 4 3 4 1 7 4 1 6 10 3
2458 1 4 3 4 1 4 8 10 3 9 2 1 4 3 4 1 8 7 10 4 9 2
2467 1 4 3 4 1 9 1 8 1 5 10 1 4 3 4 1 8 7 9 8 10 2
2458 1 4 3 4 1 8 10 1 9 8 2 1 4 3 4 1 5 4 8 3 10 1
2478 1 4 3 4 1 8 9 4 9 5 9 1 4 3 4 1 6 8 6 10 7 9
2567 1 4 3 4 1 9 2 4 8 1 10 1 4 3 4 1 6 8 6 9 3 10
2568 1 4 3 4 1 8 9 4 10 1 10 1 4 3 4 1 5 10 5 4 10 5
2578 1 4 3 4 1 8 9 10 3 10 4 1 4 3 4 1 7 8 7 10 7 9
2678 1 4 3 4 1 8 6 4 10 5 9 1 4 3 4 3 10 6 9 8 5 9
3456 1 4 3 4 1 7 8 3 8 5 10 1 4 3 4 1 8 2 8 10 3 10
3457 1 4 3 4 1 8 3 4 3 5 8 1 4 3 4 1 4 1 5 9 8 7
3458 1 4 3 4 1 7 4 3 9 1 10 1 4 3 4 1 4 1 7 9 8 5
3467 1 4 3 4 1 7 4 3 10 5 9 1 4 3 4 1 4 2 10 4 10 1
3468 1 4 3 4 1 8 7 4 8 10 8 1 4 3 4 1 4 9 8 9 2 1
3478 1 6 3 4 1 6 8 2 9 5 9 1 4 3 4 1 5 10 1 9 1 6
3567 1 4 3 4 1 9 4 8 1 6 10 1 4 3 4 1 8 9 4 10 1 6
3568 1 4 3 4 1 6 8 2 10 1 10 1 4 3 4 1 6 4 8 2 10 1
3578 1 4 3 4 1 8 2 10 3 10 4 1 4 3 4 1 8 2 8 9 7 9
3678 1 4 3 4 2 4 1 8 5 9 4 1 4 3 4 2 4 1 9 8 5 9
4567 1 4 3 4 1 9 2 4 3 9 2 1 4 3 4 1 6 8 2 10 1 6
4568 1 4 3 4 1 9 4 8 3 9 2 1 4 3 4 1 4 9 8 10 4 1
4578 1 4 3 4 10 3 9 7 10 2 10 1 4 3 4 10 1 6 10 7 9 10
4678 1 4 3 4 10 1 6 10 5 10 2 1 4 3 4 8 9 1 9 5 10 8
5678 1 4 3 4 8 9 8 7 4 1 9 1 4 3 4 2 8 9 4 1 8 7
CORNERS: (15). COSET: G(24). page 7
1234 1 4 3 9 1 7 10 3 4 5
1235 1 4 3 9 1 4 1 6 4 8
1236 1 4 3 9 2 9 1 10 4 3
1237 1 4 3 10 1 9 8 5 9 10
1238 1 4 3 9 10 6 4 3 10 1
1245 1 4 3 9 1 4 1 4 8 2
1246 1 4 3 9 1 9 3 4 10 8
1247 1 4 3 9 8 2 10 3 9 3
1248 1 4 1 4 3 10 8 5 10 2
1256 1 4 3 9 4 10 8 3 10 1
1257 1 4 3 10 1 8 7 9 8 10
1258 1 4 1 4 2 1 10 5 4 8
1267 1 4 3 9 1 10 5 9 4 2
1268 1 4 3 10 1 8 7 10 4 9
1278 1 4 3 9 1 8 9 3 10 2
1345 1 4 3 9 1 8 1 7 8 1
1346 1 4 3 9 3 10 2 8 10 7
1347 1 4 3 10 1 4 10 4 10 1
1348 1 4 3 10 8 3 8 3 9 6
1356 1 4 3 9 2 10 5 9 4 3
1357 1 4 3 9 5 4 3 9 4 9
1358 1 4 3 10 1 8 5 10 4 2
1367 1 4 3 9 2 8 9 3 10 3
1368 1 4 3 9 5 4 3 10 8 10
1378 1 4 3 9 5 10 8 5 9 10
1456 1 4 3 9 3 10 4 2 4 7
1457 1 4 3 10 1 6 10 6 9 1
1458 1 4 3 10 1 10 6 9 10 1
1467 1 4 3 10 4 9 10 3 8 5
1468 1 4 3 10 3 4 10 6 9 3
1478 1 4 3 10 4 6 10 3 4 7
1567 1 4 3 9 4 1 8 6 9 3
1568 1 4 3 9 4 2 1 10 8 3
1578 3 8 9 3 10 8 7 4 10 7
1678 1 4 9 1 10 4 5 8 10 5
2345 1 4 3 10 1 10 8 5 4 8
2346 1 4 3 9 1 9 1 9 4 6
2347 1 4 3 9 1 4 2 1 9 10
2348 1 4 3 9 1 4 1 9 10 6
2356 1 4 3 9 1 4 2 9 10 5
2357 1 4 3 9 10 8 9 3 10 1
2358 1 4 3 9 10 2 4 7 9 1
2367 1 4 3 9 6 8 9 3 8 7
2368 1 4 3 10 1 9 3 6 4 1
2378 1 4 3 4 10 2 4 3 8 7
2456 1 4 3 9 1 4 3 7 8 3
2457 1 4 3 9 1 8 1 4 1 5
2458 1 4 3 9 1 8 7 9 2 10
2467 1 4 3 9 1 8 7 10 6 9
2458 1 4 3 9 1 5 8 1 4 5
2478 1 4 3 9 4 9 10 7 10 1
2567 1 4 3 4 2 8 5 10 8 3
2568 1 4 3 10 1 8 10 4 9 1
2578 1 4 3 10 4 8 2 3 4 7
2678 1 4 1 4 9 1 10 5 9 6
3456 1 4 3 9 4 3 10 5 9 10
3457 1 4 3 9 1 6 4 6 8 5
3458 1 4 3 9 1 4 6 4 8 5
3467 1 4 3 9 1 9 8 9 4 5
3468 1 4 3 9 1 8 9 6 10 5
3478 1 4 3 2 8 7 9 1
3567 1 4 3 9 1 8 9 4 8 5
3568 1 4 3 9 1 10 2 9 4 5
3578 1 4 3 10 1 9 8 9 10 1
3678 1 4 3 9 8 9 8 3 4 5
4567 1 4 3 9 3 8 6 8 10 7
4568 1 4 3 9 1 5 4 5 8 5
4578 1 4 3 9 4 9 4 7 9 1
4678 1 4 3 9 8 2 9 3 4 7
5678 1 9 10 8 3 9 4 3 9 1
MOVES IN THE SQUARES GROUP WHICH FIX CORNERS.
KEY: 1=L; 2=F; 3=R; 4=B; 5=U; 6=D (ALL 180 DEGREE TURNS).
THE NUMBERS ON THE RIGHT GIVE THE PERMUTATION OF EACH SLICE.
THE ORDER IN WHICH SLICES ARE CONSIDERED IS FB,UD,LR.
FB SLICE: 1=LU, 2=LD, 3=RD, 4=RU.
UD SLICE: 1=LB, 2=LF, 3=RF, 4=RB.
LR SLICE: 1=FU, 2=FD, 3=BD, 4=BU.
THE NUMBER ON EXTREME RIGHT IS THE QUANTITY OF SYMMETRICALLY EQUIVALENT
POSITIONS
PAGE 1: AT LEAST ONE SLICE FIXED.
FB UD LR
1 2 1 2 1 2 1 2 1 2 1 2 1
1 2 1 2 1 2 1 2 1 3 4 3 (12) (34) 12
1 2 1 2 1 2 1 2 1 4 3 4 (12)(34) 6
1 2 1 2 1 2 1 2 3 2 1 4 (12)(34) (12)(34) 3
1 2 1 2 1 2 1 3 5 1 3 6 (12) (1324) 24
1 2 1 2 1 3 2 5 1 4 1 5 (12)(34) (123) 48
1 2 1 2 1 3 2 5 2 3 2 5 (1234) (12) 24
1 2 1 2 1 3 4 5 1 4 3 6 (123) 24
1 2 1 2 1 3 4 5 2 1 4 6 (24) (12) 24
1 2 1 2 1 5 1 2 5 2 1 5 (23) (12) 6
1 2 1 2 1 5 1 2 6 4 3 6 (14) (12) 6
1 2 1 2 1 5 2 1 2 5 2 1 (14) (12) 24
1 2 1 2 1 5 2 1 4 6 4 1 (1243) (12) 24
1 2 1 2 3 2 5 1 3 2 4 5 (1324) (1423) 12
1 2 1 2 3 5 1 4 5 4 3 6 (23) (1423) 24
1 2 1 2 4 1 2 1 5 1 3 6 (12)(34) (13)(24) 6
1 2 1 2 4 1 2 5 2 4 5 1 (14)(23) (14)(23) 6
1 2 1 2 4 1 4 1 5 1 3 5 (13)(24) (13)(24) 3
1 2 1 2 4 1 5 1 3 5 4 3 (13)(24) (12)(34) 6
1 2 1 2 4 3 2 5 6 3 5 6 (12)(34) (12)(34) 6
1 2 1 2 4 3 5 2 5 4 6 1 (1234) (12) 24
1 2 1 2 4 5 1 2 1 2 4 5 (13)(24) (134) 48
1 2 1 2 4 5 1 3 2 3 2 6 (1432) (1423) 24
1 2 1 2 4 5 1 4 1 2 4 6 (14)(23) (142) 48
1 2 1 2 4 5 2 5 3 4 6 1 (1234) (12) 24
1 2 1 2 5 1 3 6 4 3 2 1 (13)(24) 3
1 2 1 2 5 1 4 3 2 4 5 1 (1324) (24) 24
1 2 1 2 5 1 5 2 1 5 2 1 (13) (24) 12
1 2 1 2 5 1 5 2 5 2 1 5 (123) (142) 48
1 2 1 2 5 1 5 2 6 4 3 6 (134) (142) 48
1 2 1 2 5 2 1 5 1 2 5 2 (12) (13) 24
1 2 1 2 5 2 1 5 1 4 6 4 (1324) (13) 24
1 2 1 2 5 2 5 4 6 3 4 1 (1243) (12) 24
1 2 1 3 5 1 2 1 2 4 6 2 (1423) (1342) 24
1 2 1 3 5 1 2 5 2 3 5 3 (1324) (1432) 24
1 2 1 3 5 1 3 2 5 2 5 3 (1432) (1432) 12
1 2 1 5 2 5 1 5 1 2 5 2 (142) (123) 48
1 2 1 5 2 5 1 5 1 4 6 4 (243) (123) 48
2 1 2 1 3 5 1 2 5 2 3 5 3 2 (1324) (5867) 6
4 1 2 1 3 5 1 2 5 2 3 5 3 4 (1324) (5768) 6
End of execution.
MOVES IN THE SQUARES GROUP WHICH FIX CORNERS.
KEY: 1=L; 2=F; 3=R; 4=B; 5=U; 6=D (ALL 180 DEGREE TURNS).
THE NUMBERS ON THE RIGHT GIVE THE PERMUTATION OF EACH SLICE.
THE ORDER IN WHICH SLICES ARE CONSIDERED IS FB,UD,LR.
FB SLICE: 1=LU, 2=LD, 3=RD, 4=RU.
UD SLICE: 1=LB, 2=LF, 3=RF, 4=RB.
LR SLICE: 1=FU, 2=FD, 3=BD, 4=BU.
THE NUMBER ON EXTREME RIGHT IS THE QUANTITY OF SYMMETRICALLY EQUIVALENT
POSITIONS
PAGE 2: 3 3-CYCLES
FB UD LR
1 2 1 2 5 1 5 1 2 5 2 5 (124) (123) (142) 16
1 2 1 2 5 1 5 1 2 6 4 6 (124) (134) (142) 48
1 2 1 2 5 1 5 1 4 5 2 6 (132) (134) (142) 16
1 2 1 2 5 1 5 1 4 6 4 5 (132) (123) (142) 48
1 2 1 5 2 5 2 1 5 1 5 2 (142) (123) (142) 48
1 2 1 5 2 5 2 1 5 3 5 4 (123) (243) (134) 48
1 2 1 5 2 5 2 1 6 1 6 4 (123) (134) (134) 48
1 2 1 5 2 5 2 1 6 3 6 2 (142) (142) (142) 48
1 2 1 5 2 5 2 3 5 1 6 2 (142) (142) (123) 96
1 2 1 5 2 5 2 3 5 3 6 4 (123) (134) (243) 96
MOVES IN THE SQUARES GROUP WHICH FIX CORNERS.
KEY: 1=L; 2=F; 3=R; 4=B; 5=U; 6=D (ALL 180 DEGREE TURNS).
THE NUMBERS ON THE RIGHT GIVE THE PERMUTATION OF EACH SLICE.
THE ORDER IN WHICH SLICES ARE CONSIDERED IS FB,UD,LR.
FB SLICE: 1=LU, 2=LD, 3=RD, 4=RU.
UD SLICE: 1=LB, 2=LF, 3=RF, 4=RB.
LR SLICE: 1=FU, 2=FD, 3=BD, 4=BU.
THE NUMBER ON EXTREME RIGHT IS THE QUANTITY OF SYMMETRICALLY EQUIVALENT
POSITIONS
PAGE 3: NO SLICE FIXED; 2 3-CYCLES AND ONE DOUBLE TRANSPOSITION.
FB UD LR
1 2 1 2 5 1 5 2 5 4 1 6 (14)(23) (142) (134) 96
1 2 1 2 5 1 5 2 6 2 3 5 (14)(23) (243) (134) 96
1 2 1 2 5 1 5 4 5 4 3 5 (13)(24) (243) (134) 48
1 2 1 2 5 1 5 4 6 2 1 6 (13)(24) (142) (134) 48
1 2 1 5 2 5 1 5 3 2 6 2 (134) (243) (13)(24) 48
1 2 1 5 2 5 1 5 3 4 5 4 (123) (243) (13)(24) 48
1 2 1 5 2 5 2 1 2 6 3 6 (142) (12)(34) (142) 96
1 2 1 5 2 5 2 1 4 5 3 5 (123) (14)(23) (134) 96
End of execution.
MOVES IN THE SQUARES GROUP WHICH FIX CORNERS.
KEY: 1=L; 2=F; 3=R; 4=B; 5=U; 6=D (ALL 180 DEGREE TURNS).
THE NUMBERS ON THE RIGHT GIVE THE PERMUTATION OF EACH SLICE.
THE ORDER IN WHICH SLICES ARE CONSIDERED IS FB,UD,LR.
FB SLICE: 1=LU, 2=LD, 3=RD, 4=RU.
UD SLICE: 1=LB, 2=LF, 3=RF, 4=RB.
LR SLICE: 1=FU, 2=FD, 3=BD, 4=BU.
THE NUMBER ON EXTREME RIGHT IS THE QUANTITY OF SYMMETRICALLY EQUIVALENT
POSITIONS
PAGE 4: NO SLICE FIXED; AT LEAST TWO DOUBLE TRANSPOSITIONS
FB UD LR
1 2 1 2 1 3 2 1 2 1 5 6 (13)(24) (13)(24) (14)(23) 6
1 2 1 2 1 3 2 1 2 5 6 3 (13)(24) (14)(23) (14)(23) 6
1 2 1 2 1 3 2 1 5 6 4 3 (13)(24) (12)(34) (14)(23) 3
1 2 1 2 1 3 2 3 4 3 5 6 (13)(24) (13)(24) (13)(24) 1
1 2 1 2 1 3 2 5 1 2 1 6 (13)(24) (13)(24) (243) 24
1 2 1 2 1 3 4 3 4 1 5 6 (14)(23) (13)(24) (14)(23) 3
1 2 1 2 1 3 4 3 4 5 6 3 (14)(23) (14)(23) (14)(23) 6
1 2 1 2 1 3 4 5 1 2 3 5 (14)(23) (13)(24) (243) 48
1 2 1 2 1 3 5 2 1 2 6 3 (234) (14)(23) (14)(23) 48
1 2 1 2 1 3 5 2 3 4 5 1 (234) (14)(23) (13)(24) 48
1 2 1 2 4 1 5 2 1 2 6 2 (243) (12)(34) (14)(23) 24
1 2 1 2 4 5 1 2 5 6 1 5 (12)(34) (12)(34) (142) 24
1 2 1 2 5 2 4 5 4 3 2 1 (12)(34) (14)(23) (14)(23) 2
1 2 3 4 5 2 1 2 1 3 5 1 (234) (14)(23) (12)(34) 24
End of execution.
MOVES IN THE SQUARES GROUP WHICH FIX CORNERS.
KEY: 1=L; 2=F; 3=R; 4=B; 5=U; 6=D (ALL 180 DEGREE TURNS).
THE NUMBERS ON THE RIGHT GIVE THE PERMUTATION OF EACH SLICE.
THE ORDER IN WHICH SLICES ARE CONSIDERED IS FB,UD,LR.
FB SLICE: 1=LU, 2=LD, 3=RD, 4=RU.
UD SLICE: 1=LB, 2=LF, 3=RF, 4=RB.
LR SLICE: 1=FU, 2=FD, 3=BD, 4=BU.
THE NUMBER ON EXTREME RIGHT IS THE QUANTITY OF SYMMETRICALLY EQUIVALENT
POSITIONS
PAGE 5: NO SLICE FIXED; TWO 2-CYCLES.
FB UD LR
1 2 1 2 1 2 1 5 1 5 1 5 (12) (12) (124) 48
1 2 1 2 1 2 1 5 1 6 3 6 (12) (34) (124) 48
1 2 1 2 1 2 1 5 6 3 5 6 (12) (12)(34) (12) 24
1 2 1 2 1 2 5 1 3 2 4 6 (34) (13)(24) (34) 12
1 2 1 2 1 3 5 1 5 3 6 2 (12) (13) (123) 96
1 2 1 2 1 3 5 1 6 1 5 2 (12) (24) (123) 96
1 2 1 2 1 3 5 2 5 3 2 5 (124) (34) (12) 96
1 2 1 2 1 3 5 2 6 1 4 6 (124) (12) (12) 96
1 2 1 2 1 5 1 4 5 2 3 6 (12)(34) (14) (12) 12
1 2 1 2 1 5 1 4 6 4 1 5 (12)(34) (23) (12) 12
1 2 1 2 1 5 1 5 2 5 1 5 (12) (132) (12) 24
1 2 1 2 1 5 1 5 2 6 3 6 (12) (143) (12) 24
1 2 1 2 1 5 1 6 4 5 3 6 (12) (124) (12) 48
1 2 1 2 4 3 5 1 5 4 1 5 (12)(34) (14) (14) 24
1 2 1 2 4 5 1 2 5 3 6 1 (12)(34) (12) (24) 24
1 2 1 2 4 5 1 3 2 1 2 5 (13) (13)(24) (34) 24
1 2 1 2 4 5 1 5 3 6 4 1 (12)(34) (14) (24) 24
1 2 1 2 5 1 2 1 2 4 5 3 (34) (14)(23) (13) 24
1 2 1 2 5 1 5 4 3 6 4 1 (12)(34) (13) (24) 24
1 2 1 2 5 2 3 5 1 4 6 2 (12) (24) (12)(34) 24
1 2 1 3 2 5 2 1 5 1 4 6 (13)(24) (34) (34) 24
1 2 1 3 5 1 2 3 2 4 6 4 (12) (12)(34) (14) 24
1 2 1 3 5 1 2 5 4 1 5 1 (34) (24) (13)(24) 24
1 2 1 3 5 1 3 2 5 4 5 1 (13) (24) (13)(24) 12
1 2 1 3 5 1 5 1 2 1 4 6 (24) (23) (234) 96
1 2 1 3 5 1 5 3 2 1 2 6 (13) (23) (132) 96
1 2 1 5 1 5 1 2 5 2 5 1 (24) (132) (24) 48
1 2 1 5 1 5 1 2 6 4 6 1 (24) (234) (24) 48
1 2 1 5 2 1 5 1 4 6 4 1 (13)(24) (23) (12) 6
1 2 1 5 2 1 6 1 4 6 2 3 (13)(24) (14) (12) 6
End of execution.
MOVES IN THE SQUARES GROUP WHICH FIX CORNERS.
KEY: 1=L; 2=F; 3=R; 4=B; 5=U; 6=D (ALL 180 DEGREE TURNS).
THE NUMBERS ON THE RIGHT GIVE THE PERMUTATION OF EACH SLICE.
THE ORDER IN WHICH SLICES ARE CONSIDERED IS FB,UD,LR.
FB SLICE: 1=LU, 2=LD, 3=RD, 4=RU.
UD SLICE: 1=LB, 2=LF, 3=RF, 4=RB.
LR SLICE: 1=FU, 2=FD, 3=BD, 4=BU.
THE NUMBER ON EXTREME RIGHT IS THE QUANTITY OF SYMMETRICALLY EQUIVALENT
POSITIONS
PAGE 6: NO SLICE FIXED; TWO 4-CYCLES
FB UD LR
1 2 1 2 1 2 1 2 4 1 5 6 (1324) (13)(24) (1423) 12
1 2 1 2 1 2 1 2 4 5 6 3 (1324) (14)(23) (1423) 24
1 2 1 2 1 3 4 5 2 3 4 5 (1234) (13)(24) (1324) 24
1 2 1 2 1 3 5 1 2 1 6 3 (1423) (14)(23) (1432) 24
1 2 1 2 1 3 5 1 2 5 1 6 (1423) (1324) (243) 48
1 2 1 2 1 3 5 1 2 6 3 5 (1423) (1423) (243) 48
1 2 1 2 1 3 5 1 5 1 6 4 (1423) (1432) (243) 96
1 2 1 2 1 3 5 1 6 3 5 4 (1423) (1234) (243) 96
1 2 1 2 1 3 5 2 5 1 2 6 (234) (1324) (1324) 96
1 2 1 2 1 3 5 2 6 3 4 5 (234) (1423) (1324) 96
1 2 1 2 1 5 2 1 4 5 4 3 (1342) (12)(34) (1423) 24
1 2 1 2 3 5 1 2 5 2 1 6 (13)(24) (1243) (1324) 6
1 2 1 2 3 5 1 2 6 4 3 5 (13)(24) (1342) (1324) 6
1 2 1 2 3 5 1 4 5 2 3 5 (14)(23) (1342) (1324) 12
1 2 1 2 3 5 1 4 6 4 1 6 (14)(23) (1243) (1324) 12
1 2 1 2 3 5 1 5 2 5 1 6 (1423) (124) (1324) 48
1 2 1 2 3 5 1 6 4 5 3 5 (1423) (132) (1324) 24
1 2 1 2 3 5 1 6 4 6 1 6 (1423) (143) (1324) 24
1 2 1 2 4 3 5 1 2 1 6 4 (1423) (12)(34) (1342) 24
1 2 1 2 4 3 5 1 5 2 1 6 (13)(24) (1243) (1342) 24
1 2 1 2 4 5 1 5 1 6 2 1 (13)(24) (1342) (1234) 24
1 2 1 2 5 1 5 2 3 5 4 1 (14)(23) (1432) (1234) 24
1 2 1 2 5 1 5 4 1 6 2 1 (13)(24) (1432) (1234) 12
1 2 1 2 5 1 5 6 2 3 5 1 (1423) (12)(34) (1234) 24
1 2 1 2 5 2 3 5 3 2 6 4 (1423) (1234) (14)(23) 24
1 2 1 3 5 1 5 1 2 3 4 5 (1234) (1342) (143) 96
1 2 1 3 5 1 5 1 6 3 4 1 (14)(23) (1342) (1432) 24
1 2 1 3 5 1 5 3 2 3 2 5 (1432) (1342) (124) 96
1 2 1 5 1 5 3 2 5 4 6 1 (1432) (124) (1234) 48
1 2 1 5 1 5 3 2 6 2 5 1 (1432) (143) (1234) 48
End of execution.
MOVES IN THE SQUARES GROUP WHICH FIX CORNERS.
KEY: 1=L; 2=F; 3=R; 4=B; 5=U; 6=D (ALL 180 DEGREE TURNS).
THE NUMBERS ON THE RIGHT GIVE THE PERMUTATION OF EACH SLICE.
THE ORDER IN WHICH SLICES ARE CONSIDERED IS FB,UD,LR.
FB SLICE: 1=LU, 2=LD, 3=RD, 4=RU.
UD SLICE: 1=LB, 2=LF, 3=RF, 4=RB.
LR SLICE: 1=FU, 2=FD, 3=BD, 4=BU.
THE NUMBER ON EXTREME RIGHT IS THE QUANTITY OF SYMMETRICALLY EQUIVALENT
POSITIONS
PAGE 7: NO SLICE FIXED; 2-CYCLE + 4-CYCLE.
FB UD LR
1 2 1 2 1 2 1 3 5 2 4 5 (34) (13)(24) (1423) 24
1 2 1 2 1 2 1 5 2 4 5 3 (34) (14)(23) (1423) 24
1 2 1 2 1 3 2 5 2 1 2 6 (24) (13)(24) (1324) 24
1 2 1 2 1 3 5 1 2 3 5 1 (1423) (14)(23) (24) 24
1 2 1 2 1 3 5 1 3 5 1 4 (1423) (14)(23) (34) 24
1 2 1 2 1 5 1 2 5 4 1 6 (14)(23) (1342) (34) 24
1 2 1 2 1 5 1 3 2 5 4 6 (143) (1342) (34) 96
1 2 1 2 1 5 1 3 2 6 2 5 (143) (1243) (34) 96
1 2 1 2 1 5 1 4 5 4 3 5 (13)(24) (1243) (34) 24
1 2 1 2 1 5 1 5 4 5 3 5 (1423) (124) (34) 48
1 2 1 2 1 5 1 5 4 6 1 6 (1423) (234) (34) 48
1 2 1 2 1 5 1 6 2 5 1 6 (1423) (132) (34) 48
1 2 1 2 1 5 1 6 2 6 3 5 (1423) (143) (34) 48
1 2 1 2 1 5 2 1 2 6 2 3 (23) (12)(34) (1423) 24
1 2 1 2 4 1 5 1 2 1 6 2 (1324) (12)(34) (14) 24
1 2 1 2 4 1 5 1 5 4 3 5 (13)(24) (1243) (14) 24
1 2 1 2 4 1 5 2 3 5 2 5 (1234) (23) (12)(34) 24
1 2 1 2 4 1 5 2 5 2 5 3 (1234) (24) (12)(34) 24
1 2 1 2 4 3 5 2 5 2 6 3 (24) (1234) (13)(24) 24
1 2 1 2 4 5 1 5 1 5 2 3 (12)(34) (14) (1432) 24
1 2 1 2 4 5 1 5 3 5 4 3 (13)(24) (1342) (13) 24
1 2 1 2 4 5 2 5 1 4 5 1 (24) (1324) (14)(23) 24
1 2 1 2 4 5 2 5 6 1 2 5 (1234) (12)(34) (12) 24
1 2 1 2 4 5 2 5 6 3 2 6 (24) (14)(23) (1324) 24
1 2 1 2 5 1 3 2 5 1 4 5 (132) (12) (1423) 96
1 2 1 2 5 1 3 2 5 3 4 6 (143) (1423) (34) 96
1 2 1 2 5 1 3 2 6 1 2 5 (143) (1324) (34) 96
1 2 1 2 5 1 3 2 6 3 2 6 (132) (34) (1423) 96
1 2 1 2 5 1 5 1 2 4 6 4 (1324) (13) (142) 96
1 2 1 2 5 1 5 1 6 4 5 6 (12) (1234) (142) 96
1 2 1 2 5 1 5 3 2 4 6 2 (34) (1432) (134) 96
1 2 1 2 5 1 5 3 6 2 5 6 (1423) (24) (134) 96
1 2 1 2 5 1 5 6 4 1 5 3 (12) (13)(24) (1432) 24
1 2 1 2 5 2 1 5 3 2 6 2 (34) (1432) (13)(24) 24
1 2 1 2 5 2 5 2 6 1 4 1 (23) (1423) (14)(23) 24
1 2 1 3 5 1 2 1 6 2 5 6 (34) (14)(23) (1342) 24
1 2 1 3 5 1 2 3 6 4 5 6 (1324) (13)(24) (14) 24
1 2 1 3 5 2 5 2 5 3 5 6 (1234) (13) (14)(23) 24
1 2 1 5 1 5 1 2 4 5 4 3 (12)(34) (1243) (13) 24
1 2 1 5 1 5 1 2 5 4 5 3 (1234) (124) (13) 96
1 2 1 5 1 5 1 2 6 2 6 3 (1234) (143) (13) 96
1 2 1 5 1 5 2 5 2 3 6 3 (12) (132) (1432) 96
1 2 1 5 1 5 2 5 4 3 5 3 (1423) (124) (13) 96
1 2 1 5 1 5 2 6 2 1 6 3 (1423) (143) (13) 96
1 2 1 5 1 5 2 6 4 1 5 3 (12) (234) (1432) 96
1 2 1 5 1 5 3 6 2 5 6 1 (14)(23) (14) (1234) 24
A DETAILED EXAMPLE OF THE 52-MOVE STRATEGY
(UFL)+ (URF)- (UBR)+ (ULB)- (LF)* (FR)* (RB)* (BL)*
First decide on a coordinate system for the Cube
(i.e. decide which colours are L,R,F,B,U,D); then get
it into the above position.
Stage 1. There are 4 bad edge-pieces, namely in positions
LF,FR,RB,BL. Manoeuvre these to the U-face by FLR'D2B2.
Then the move U corrects them.
Summary of Stage 1:- FLR'D2B2U (6 moves).
Stage 2. The LR-slice edge pieces are now in positions
LD,FD,RD,BD. Manoeuvre these to the UD-slice by F2D2LR'F.
Now taking the corner positions in order (as in the
diagram in Stage 3 instructions), the respective twists of
the pieces in these positions are 0,2,0,2,0,0,1,1. This
combination of twists is not given in Stage 2 tables, but
a 180° rotation about the LR-axis followed by reflection
in the LR-slice transforms this to 2 2 0 0 0 1 0 1, which
is in the tables. The move given is F LFL2F'LF2BL2, and
transforming this by the above (involutory) symmetry gives
B'R'B'R2BR'B2F'R2. Therefore we perform the inverse of
this move, after which L and R faces have L and R colours
on them only.
Summary of Stage 2:- F2D2LR'FR2FB2RB'R2BRB (14 moves)
Stage 3. The positions where corners are out of orbit are
numbers 1,2,5,8. The preliminary instructions for this
stage instruct us to perform L'U2. For the remainder of
this stage alter the coordinate system so that the original
D-face faces you and the original F-face faces upwards.
In this new coordinate system the positions where corners
are out of orbit are 1,5. The permutation of corners is
(1357)(24). Multiplying this on the right by (15)(24) gives
(13)(57) which is a permutation of corners in G3. Therefore
we must refer to page 7 of the Stage 3 tables. The edge-
pieces of the FB-slice are in positions 3,4,5,8. The tables
give us LF2L'U2LF2R2F2B2R, or LD2L'F2LD2R2D2U2R in the
original coordinate system. Perform the inverse of this move.
Summary of Stage 3:- L'U2R'U2D2R2D2L'F2LD2L' (12 moves).
Stage 4. The corners are restored by L2R2(original coordinates).
Looking at edge-pieces, as no slice is fixed and there is
a 2-cycle and a 4-cycle, we refer to page 7 of the Stage 4
tables. The only entries where the correct arrangement of
pieces is permuted and the 4-cycle is of the correct type are
(143) (1342) (34) and (143) (1243) (34). If we hold the
Cube with the original R-face facing the operator, and the
original B-face uppermost, we find we have the second of these
permutations. Therefore perform the inverse of the move
given, i.e. perform B2R2F2R2D2U2B2U2R2U2R2U2in original coords.
Summary of Stage 4:- L2R2B2R2F2R2D2U2B2U2R2U2R2U2(14 moves).
Total number of moves required: 6+14+12+14 = 46. (45 with cancellation)
M.B.T.