


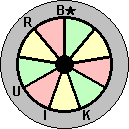
Rubik's Rabbits is a puzzle in the shape of a top hat. The hat is divided into 6 discs, which can rotate. You can look inside the hat, and see that the discs are divided into 9 segments, each of which may or may not show a rabbit when held up to the light. The aim is to turn the discs such that all nine rabbits are visible. On the outside the discs are marked with one letter each, so that their positions are clearly visible. The letters spell out *RUBIK, with the * on the rim of the hat. In the initial position when all the letters are lined up there are no rabbits visible.
The top of the hat is coloured, so that when solved the 9 visible rabbits alternate in the colours yellow, green and red. For an extra challenge you could try to get a position where only three rabbits of the same colour are visible, or where 6 rabbits are visible of only two colours.
If you consider the rim of the hat fixed, then the other 5 discs can each be in any of the 9 possible positions. There are therefore only 95 = 59,049 positions. There is only one solution.
The segments of the discs are traced out in the following table (the brim of the hat lies at the top of the table). The X and O mark the two types of polarized filters. This is the initial position. As each column has an X and an O, no segment shows a rabbit.
| * | X | X | X | ||||||||||||||
| R | X | X | X | ||||||||||||||
| U | O | O | O | ||||||||||||||
| B | O | O | O | ||||||||||||||
| I | X | X | X | ||||||||||||||
| K | O | O | O | ||||||||||||||
Note that the starting position is not the only one that shows no rabbits. You can rotate the three discs UBK as a whole any amount relative to the *RI discs, and still no rabbits would show.
The unique solved position is shown in this table. Each column has only X's or only O's.
| X | X | X | * | ||||||||||||||
| X | X | R | X | ||||||||||||||
| O | U | O | O | ||||||||||||||
| B | O | O | O | ||||||||||||||
| I | X | X | X | ||||||||||||||
| K | O | O | O | ||||||||||||||
 Here is the solution described in words:
Here is the solution described in words:
Here are solutions to the extra challenges. There are only 16, 184 and 8 solutions for three green, yellow, or red rabbits respectively.
| * | X | X | X | ||||||||||||||
| X | X | R | X | ||||||||||||||
| O | O | O | U | ||||||||||||||
| B | O | O | O | ||||||||||||||
| X | X | I | X | ||||||||||||||
| K | O | O | O | ||||||||||||||
| * | X | X | X | ||||||||||||||
| X | R | X | X | ||||||||||||||
| O | U | O | O | ||||||||||||||
| B | O | O | O | ||||||||||||||
| I | X | X | X | ||||||||||||||
| K | O | O | O | ||||||||||||||
| X | X | X | * | ||||||||||||||
| R | X | X | X | ||||||||||||||
| O | U | O | O | ||||||||||||||
| B | O | O | O | ||||||||||||||
| I | X | X | X | ||||||||||||||
| K | O | O | O | ||||||||||||||
There are 33, 133 and 2 solutions for red & yellow, yellow & green, or red & green rabbits respectively.
| X | X | X | * | ||||||||||||||
| X | R | X | X | ||||||||||||||
| O | O | U | O | ||||||||||||||
| O | O | B | O | ||||||||||||||
| I | X | X | X | ||||||||||||||
| K | O | O | O | ||||||||||||||
| * | X | X | X | ||||||||||||||
| X | X | R | X | ||||||||||||||
| O | O | O | U | ||||||||||||||
| B | O | O | O | ||||||||||||||
| X | X | X | I | ||||||||||||||
| K | O | O | O | ||||||||||||||
| X | * | X | X | ||||||||||||||
| X | R | X | X | ||||||||||||||
| O | U | O | O | ||||||||||||||
| B | O | O | O | ||||||||||||||
| I | X | X | X | ||||||||||||||
| K | O | O | O | ||||||||||||||