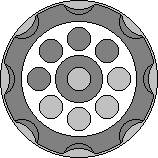
The Enigma puzzle is disc shaped with a picture or other design on the front face. There
are two outer rings around the edge of the disc which can be turned, and this causes
an internal mechanism to rotate various circular parts of the front face. The rotating
parts of the front face are 8 small discs equally spaced around the edge, and in the
centre one disc with a ring around it. In the picture on the right all the moving
pieces are coloured light or dark grey, matching the colour of the outer ring they are
connected to.
There is a little clip with the puzzle that can be attached to the edge so that
it will not be accidentally mixed up.
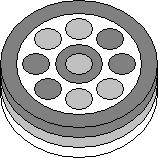The Combinescion puzzle is very similar to the Enigma, though it is shaped like a cylinder.
The base and the two turning rings are simply three disks of the same diameter and about
the same thickness stacked together. Another minor difference is that whereas the rings of
the Enigma turn four adjacent small discs, the layers of the Combinescion each turn two
adjacent pairs of small discs. This is illustrated in the picture on the right.
Note that unlike the Enigma, part of the pictorial design on
the front of the Combinescion is generally also partly printed on the top layer ring, so
not only do the small disks and the centre ring have to match up, the top layer ring
must match too.
The combinescion was invented by Roman Massimiliano, patented 1 February 1996
WO 96/02307.
Solution to Enigma:
I have opened up the Enigma puzzle to count the number of teeth on the various cogs inside.
This is not recommended, as it is hard to put back together correctly. The results are shown
in the table below:
| light grey | | | |
dark grey | |
|---|
| Middle outer ring | 105 | (21) | |
Front outer ring | 108 | (4) |
| Edge discs | 25 | (5) | |
Edge discs | 27 | (1) |
| |
| Edge discs | 26 | | | Edge discs | 28 | |
| Centre disc | 53 | | |
Centre ring | 51 | |
Solving this puzzle is quite easy.
-
Turn the front outer ring until the centre ring in the front face is correct.
-
If the edge discs that are also controlled by the front outer ring are not correct,
then turn the front outer ring clockwise until the next time the centre ring is again
correct. Repeat this if necessary, until all the parts controlled by the front outer
ring are correct. This need not be done more than 28 times, since if the centre ring
has done 28 revolutions then the small discs will have done 51 revolutions exactly
and be in their original orientations.
- Turn the middle outer ring until the centre disc in the front face is correct.
- If the edge discs that are also controlled by the middle outer ring are not correct,
then turn the middle outer ring clockwise until the next time the centre disc is again
correct. Repeat this if necessary, until all the parts controlled by the middle outer
ring are correct. This need not be done more than 26 times, since if the centre disc
has done 26 revolutions, then the small discs will have done 53 revolutions exactly
and be in their original orientations.
- The front face should now be solved.
Note that the front outer ring will automatically be in the right position for the
locking clip to be attached, because of the 4:1 ratio of cog teeth, and the fact that
there are exactly 8 finger grips in the outer ring.
Solution to Combinescion:
The Combinescion could not be opened, so I deduced the number of teeth on the cogs from
the gearing ratio's. The numbers are different to the Enigma.
| light grey | | |
dark grey | |
|---|
| Middle layer | 80 | |
Top layer | 82 |
| Edge discs | 19 | |
Edge discs | 21 |
| |
| Edge discs | 19 | |
Edge discs | 21 |
| Centre disc | 42 | |
Centre ring | 40 |
Solving Combinescion is similar to the Enigma:
- Turn the top layer ring until its design matches up with the rest
of the front face.
- If the centre ring in the front face is not correct,
then turn the top layer ring clockwise one full revolution clockwise. Repeat this
until the centre ring is matched up correctly. You never need to turn more than 20
times, since if the top layer has done 20 revolutions then the small centre ring
will have done 41 revolutions exactly and be in its original orientation.
- If the edge discs that are also controlled by the top layer
are not correct, then turn the top layer ring clockwise for 20 revolutions, until the
next time the centre ring is again correct. Repeat this if necessary, until all the
parts controlled by the top layer ring are correct. This need not be done more than 21
times, so the total number of turns of the top layer is no more than 20·21=420.
- Turn the middle layer until the centre disc in the front
face is correct.
- If the edge discs that are also controlled by the middle
layer are not correct, then turn the middle layer clockwise until the next time the
centre disc is again correct. Repeat this if necessary, until all the parts controlled
by the middle layer ring are correct. This need not be done more than 19 times, since
if the centre disc has done 19 revolutions then the small discs will have done 42
revolutions exactly and be in their original orientations.
- The front face should now be solved.
