


This puzzle consists of a square 3×3 tray with eight cubes in it. The cubes are identical, and each side of a cube is a different colour. There are ridges on the base of the tray so if you push a cube towards the vacant space it will easily roll over. By rolling the cubes around they get mixed up. The aim is to arrange them so that the space is in the middle and that the cubes show all the same colour on top. A more difficult challenge is to have the space in the middle and all the cubes in the exact same orientation, i.e. not only do the top faces match, the sides match as well.
The puzzle was invented by John Harris, and discussed in Martin Gardner's Mathematical Games column in the Scientific American, March and April 1975. In that original version only the top faces of the cubes are coloured, and the aim is to find the shortest sequence that leaves all the cubes turned upside down, with the gap in the middle. A more difficult version is mentioned too, in which all 24 outwardly visible faces are red, all 24 unexposed faces (i.e. touching faces and bottom sides) are not coloured. Here the aim is to go from being completely red on the outside to completely uncoloured. By the way, the inventor is not the same John Harris who invented the Astrolabacus puzzle.
If your browser supports JavaScript, then you can play the Eight Cubes Puzzle by clicking the link below:
Suppose you only want to solve one colour on top. Each cube has 6 sides where this
colour can be. The eight cubes therefore have 68=1,679,616 possible
orientations. Their permutation does not matter, except for the position of the
vacant space. There are thus 9·68 = 15,116,544 positions.
If you want to solve all the colours then it matters where they are, and so the
cubes each have 24 possible orientations. The permutation of the cubes again does
not matter as they are identical. The total number of positions is therefore at most
9·248=990,677,827,584. Not all these positions can be achieved
however because there is an awkward parity constraint. A cube orientation has an even
or odd parity according to whether an even or an odd number of quarter turns are needed
to fix it. A cubes orientation parity will then depend on its position in the tray
compared to its starting position. The cubes therefore split into two sets of four,
those that started at a corner and those that started at an edge. There are
9!/4!2 = 630 ways to permute the two sets in the tray, giving a total of
only 630·128=270,888,468,480 positions.
I have let my computer calculate God's Algorithm for the version of this puzzle where only the top faces of the eight cubes are coloured. The results are shown in the table below.
|
|
|
The 12 antipodal positions are rotations/reflections of the following two patterns:
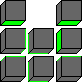
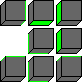
In the previous table rolling any cube one step is counted as one move. If instead we only consider positions with the space in the centre, and count the simple sequences of 4 moves that keep the space in the centre, then the result is as shown below.
| Depth | Positions |
|---|---|
| 0 | 1 |
| 1 | 8 |
| 2 | 44 |
| 3 | 248 |
| 4 | 1,338 |
| 5 | 7,084 |
| 6 | 34,580 |
| 7 | 143,588 |
| 8 | 409,552 |
| 9 | 601,887 |
| 10 | 371,928 |
| 11 | 96,678 |
| 12 | 11,878 |
| 13 | 796 |
| 14 | 6 |
| Total: | 1,679,616 |
| Avg Depth | 8.8611 |
The 6 antipodal positions are rotations/reflections of the following two patterns:
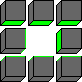
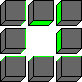
Solving one colour only:
This solution places a single colour on top. The colours around the sides remain mixed.
Solving all colours:
This solution orients the cubes exactly the same, so that the colours around the sides match too.
If the cubes have been randomly placed in the tray the it is likely not possible, so only try this if the puzzle has been mixed from the starting position.